燕尾定理:在三角形abc中,ad,be,cf相交于同一点o,有s aob∶s aoc=bd∶cds aob∶s cob=ae∶ces boc∶s aoc=bf∶af因此图类似燕尾而得名。是五大模型之一,是一个关于平面三角形的定理,俗称燕尾定理。解 aas 三角形 用 三角形三个内角的和是 180° 来求剩下来的角度;三角形の3辺から角度を計算 にリンクを張る方法 ホーム / 数学公式集 / 三角関数(度) このページの先頭へ ブックマーク 実行履歴 関連ライブラリ 三角関数(度) 三角関数(グラフ) 逆三角関数(度) 角度と底辺から斜辺と高さを計算 角度と高さから底辺と斜辺を計算 角度と斜辺
70以上三角形3 4 5 角度 シモネタ
円 三角形 角度 定理
円 三角形 角度 定理- 已知不规则三角形三边长求角度的公式 回答作者:清川带长薄清川带长薄 采纳时间: 0727 cosA=(b平方c平方a平方) /2cb cosB=(a平方c平方b平方)/2ac cosC=(a平方b平方c平方)/2ab 这是余弦定理 网友问题:三角形知道三边求角度? 回答作者:青山常有雾青山常有雾 采纳时间: 0727三角形解了――我们知道所有的角度和边长了。 三角形可以可以用其他的英语字母而不用 ABC: 例 2 这个也是 SSS 三角形。 在这三角形我们知道三条边:x = 51、y = 79 和 z = 35。先用余弦定理来求 角 X: cos X = (y 2 z 2 − x 2)/2yz cos X = ((79) 2 (35) 2 − (51) 2)/(2×79×35) cos X = (6241 1225 − 2601)/553




三角形的度数是多少 边分别是345的三角形的度数分别是多少 三人行教育网 Www 3rxing Org
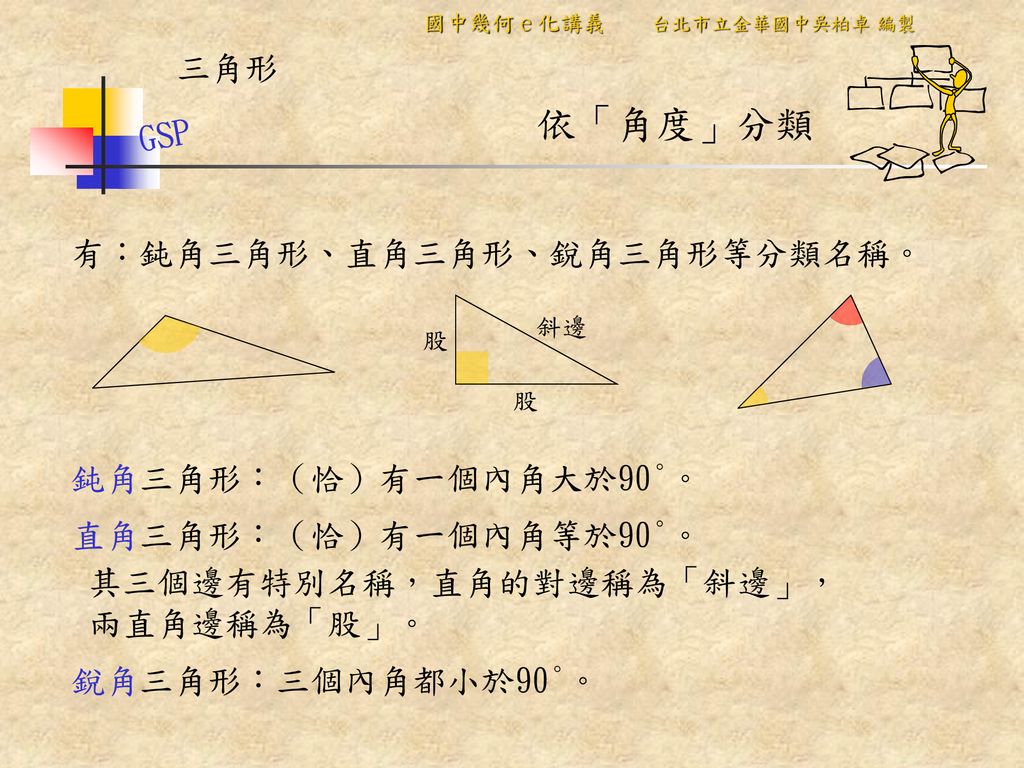
直角三角形の定義とさまざまな公式 レベル ★ 基礎 平面図形 三角比・三角関数 更新日時 直角三角形 とは,1つの角が直角である三角形のことです。 直角三角形のさまざまな性質を紹介します。 目次 三平方の定理(ピタゴラスの定理) 1、直角三角形两直角边的平方和等于斜边的平方。 2、在直角三角形中,两个锐角互余。 3、直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。 该性质称为直角三角形斜边中线定理。 4、直角三角形的两 三角形 \(ABC\) について、点 \(A,B,C\) の内角をそれぞれ角 \(A,B,C\) とおき アタリマエ! 統計学 パッと見で分かる統計学ノート;
C = 7。 用余弦定理(角度形式)来求角 C: cos C = (a 2 b 2 − c 2)/2ab = (8 2 6 2 − 7 2)/2×8×6 = (64 36 − 49)/96 = 51/96 = C = cos1 () = 579° 保留一位小数 a、b 和 c 的形式 你也可以重写 c 2 = a 2 b 2図形 定義・定理 まとめ 対頂角 𝟖は等しい 直線の角度 ° 平行線の 同位角 𝟖 は等しい 角形の内角の和 °×(𝒏− ) 平行線の 多角形の外角の和錯角 𝟔は等しい ° 同位角 が等しければ、2直線は平行 〇 合同な図形の対応する線分や角は等し い。 錯角 が等しければ、2直線は平行 三角形 四角形三角形の「2 辺 (ただし、正弦定理で"角度"を求めると、次の答案のように解が2つ出てくることがあります。そのとき、2つとも解であることも、1つだけが解で他方は解でないこともあります。 ac>180 ° のようなときは、その解は不適当です。) (解答) より、 c=60 °, 1 ° ・・・(答
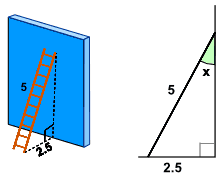
从已知两边求角度 若我们知道 直角三角形 两条边的长度,我们便可以求三角形的未知角度。 例子 梯子搁在墙上,如图。 梯子与墙之间的 角度 是多少?如果给出足够的几何属性,任意三角形计算器就能自动补全任意三角形的所有属性,例如面积,周长,边和角度。 三角形是具有三个顶点(角)和三条边(边)的多边形。 任意三角形 维基百科页面相关计算器:等边三角形计算器等腰三角形计算器直角三角形计算器紙に書いた三角形を切って確認することですが ここではもう少し論理的に確認していこうと思います。 上の図は適当に書きましたので、 私にもそれぞれの角度がどれくらいか分かりません。 でも、内角の和は求められます。



高中数学 余弦定理的详细使用方法 掌握了做题速度特快




直角三角形知道两边求角度 每日一讲 解直角三角形 3 21 半次元的博客 Csdn博客
(1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の2辺と一つの角度から他の角の大きさを求める これは、「パターン1:三角形の3辺の長さから角度を求める」の応用で求めることができます。 まず、余弦定理を使って、長さが不明である辺の長さを求めます。高一数学必修5第一章解三角形教学设计 三明九中 林晴岚 一课标要求 本章的中心内容是如何解三角形,正弦定理和余弦定理是解三角形的工具,最后落实在解三角形的应用上。通过本章学习,学生应当达到以下学习目标: 1通过对任意三角形边长和角度关系的探,新文库网




如何在余弦定理中找到余弦 数学21




1 3 範例5 餘弦定理sss求角度 Youtube
/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l e (1) cosタレスの定理(タレスのていり、英 Thales' theorem )とは、直径に対する円周角は直角である、つまり、A, B, C が円周上の相異なる 3 点で、線分 AC が直径であるとき、∠ABC が直角であるという定理である。 ターレスの定理、タレースの定理ともいう。 歴史 古代ギリシャの哲学者、数学者タレス 任意三角形边长与角度的关系 三角形的角度与各个边的长度关系 角度与各边的长度关系 三角形的三个内角为角A、角B、角C,则它们分别所对的边为a、b、c。并且,大边对大角,大角对大边。若角A大于角B,则a大于b。若三角形的三个角均相等,则三条边也相等
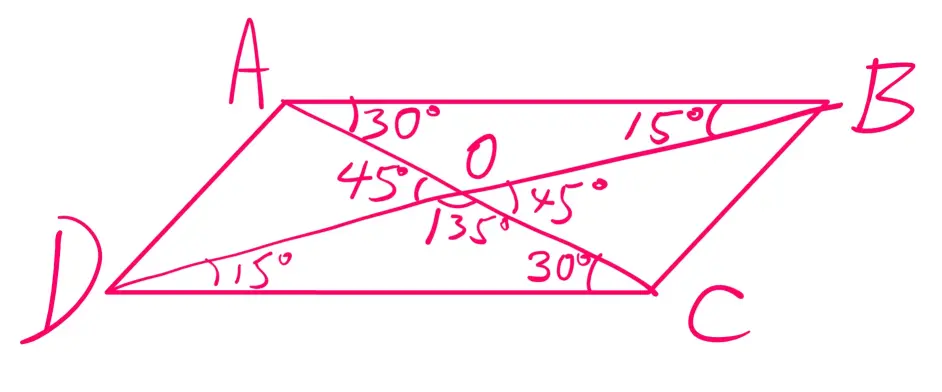



求角 Dac 平行四边形性质定理与各种角的和差关系都试过 也搞不出来 哔哩哔哩



已知三角形三条边a B C的长度 那么请问该三角形的三个角分别是多少度 秦学教育
这三角形可以用 三角形的角 来求剩下的角,然后用 正弦定理 来求其他两个边长。去 解 "aas" 三角形 看看。 三、asa 已知两个角度 和 一个在这两个角之间的边长。 我们用 三角形的角 来求第三个角,然后用 正弦定理 来求另外两条边的长度。去 解 "asa" 三角形好,今天你学习了《AMC系列》的第五讲,了解了关于圆的角度和长度,也明白了它们之间相互组合又能形成什么更有趣的定理。 恭喜你,又解锁了AMC数学竞赛的一个新章节。 下次我们将学习坐标系。 你可能错过了之前的课程: AMC 三角形的这 4 颗心,我们 直角三角形とは? 定義や定理、辺の長さの比、合同条件 21年2月19日 この記事では、「直角三角形」の定義や合同条件、重要な辺の長さの比について解説していきます。 また証明問題もわかりやすく説明していくので、ぜひマスターしてくださいね



解三角形




三四五三角形角度 边长为3 4 5的直角三角形的角度分别为什么 三人行教育网 Www 3rxing Org
余弦定理是解三角形中的一个重要定理,可应用于以下三种需求: 当已知三角形的两边及其 夹角 ,可由余弦定理得出已知角的 对边 。凹四角形の角度の関係 a x = 4 角の二等分線に関係する辺の比や長さ b ab ac = be ec = bf cf ae=√ab×ac−be×ec 5 正三角形の辺と高さの比、面積 a h= √3 2 a (面積)= 2 √3 4 a 6 方べきの定理(全3 パターン)c pa×pd=pb×pc pa×pd= pb2 pa×pc=pb×pd 7 頂角が等しい二つの三角形の面積比 b apq abc = ap×aq 问题 4 :证明 三角形内角和定理:三角形 的三个内角和等于 180 º; 已知:如图 2 , 求证:∠ a ∠ b ∠ c= 教师引导学生对拼合的图形进行分析,得出辅助线的做法及证明的思路。 设计意图 教师指导学生从不同角度思考,展示证法的多样性。通过定理的证明使学生感受几何证明的思想




直角三角形边角换算 直角三角形知道边长角度怎么算 三人行教育网 Www 3rxing Org




如何使用勾股定理 12 步骤
余弦定理对解三角形 是 例子:用余弦定理(角度形式)来求角 "C" 已知三边: a = 8, b = 6 和 ; 実は、ピタゴラスの定理を応用した「三角測量」も、私たちの身近なところで活用されているんです。 2つの角度がわかれば、三角形が確定し、距離がわかる 位置と距離のわかる2直角三角形 110 /2件 表示件数 5 10 30 50 100 0 1 1245 60歳以上 / その他 / 非常に役に立った /



勾股三角形各角的度数 西瓜视频搜索




小学生都知道的三角形内角和 到了初一一定要掌握的五种证明 每日头条



餘弦定理 维基百科 自由的百科全书



1



三角形外角定理 腾讯视频



等腰三角形求度数的公式一些有关于求三角形度数的公式 完整点 朵拉利品网
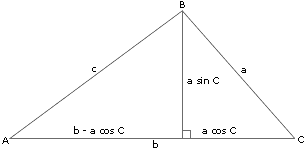



餘弦定理 维基百科 自由的百科全书




高考数学考点之正 余弦定理及解三角形 王羽课堂



等腰三角形角度是多少等腰三角形的性质定理及其证明 范文大全




06 圆周角定理 相似三角形的定理与圆幂定理高中数学 Youtube




角与边的关系三角函数 三角函数sin Cos Tan各等于什么边比什么边 三人行教育网 Www 3rxing Org




直角三角形知道两边求角度 每日一讲 解直角三角形 3 21 半次元的博客 程序员宅基地 程序员宅基地



三角形 维基百科 自由的百科全书
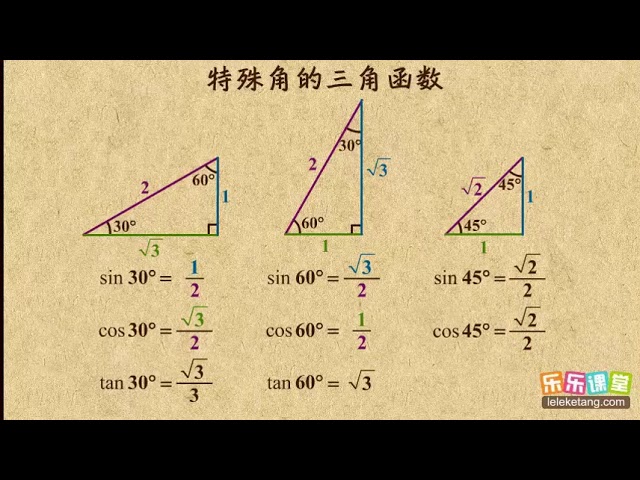



02特殊角的三角函数直角三角形的边角关系初中数学初三 Youtube



已知三角形三条边a B C的长度 那么请问该三角形的三个角分别是多少度 秦学教育




三角形的度数是多少 边分别是345的三角形的度数分别是多少 三人行教育网 Www 3rxing Org



梅涅劳斯定理 共角三角形的三边关系 雪花新闻




证明三角形中的三个一半定理



几何长度 角度关系沟通的桥梁自然是基本定理 定律 法则 公式



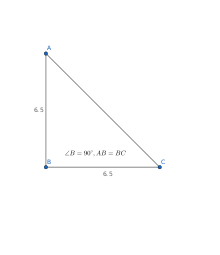
求直角三角形的角度
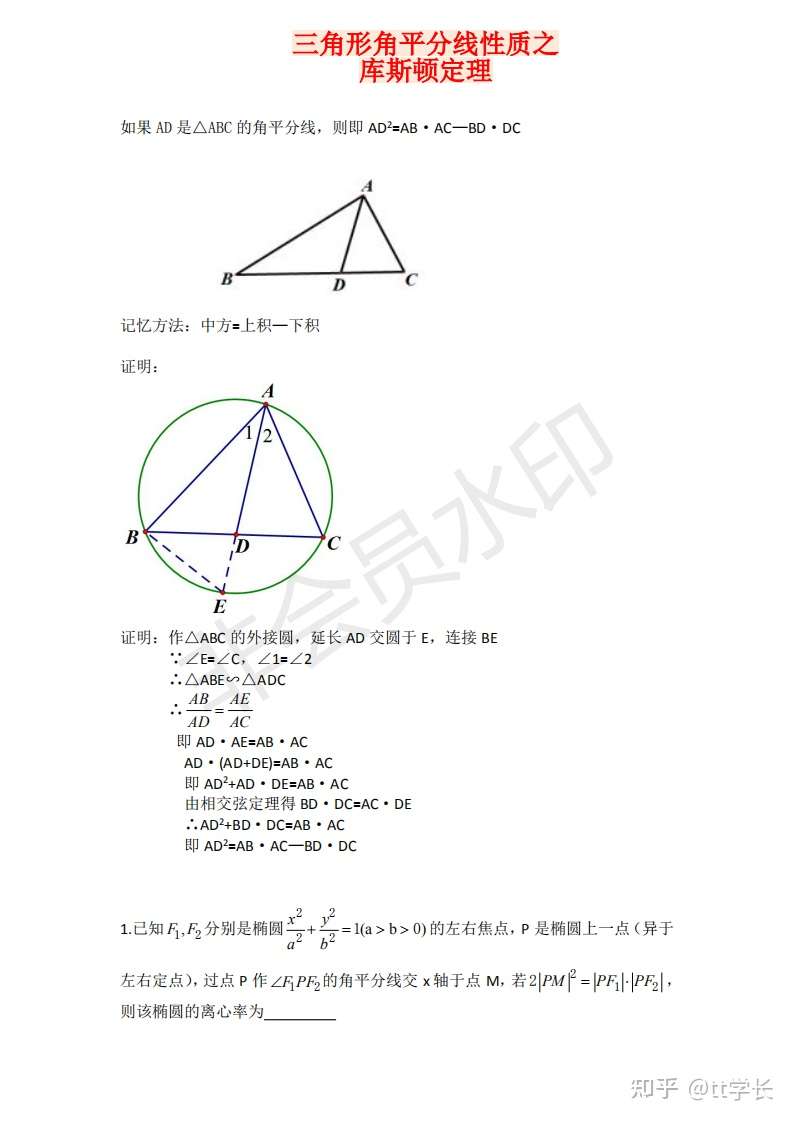



解三角形角平分线秒杀技巧之 斯库顿定理 一个超实用的干货 知乎
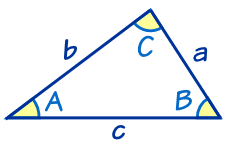



余弦定理




枢纽定理 Wikiwand



Q Tbn And9gcromkb8c Qm5e9wjbzechamldnebgbei7cyrlr87pqeumwoh98e Usqp Cau
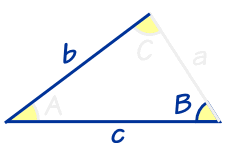



解三角形
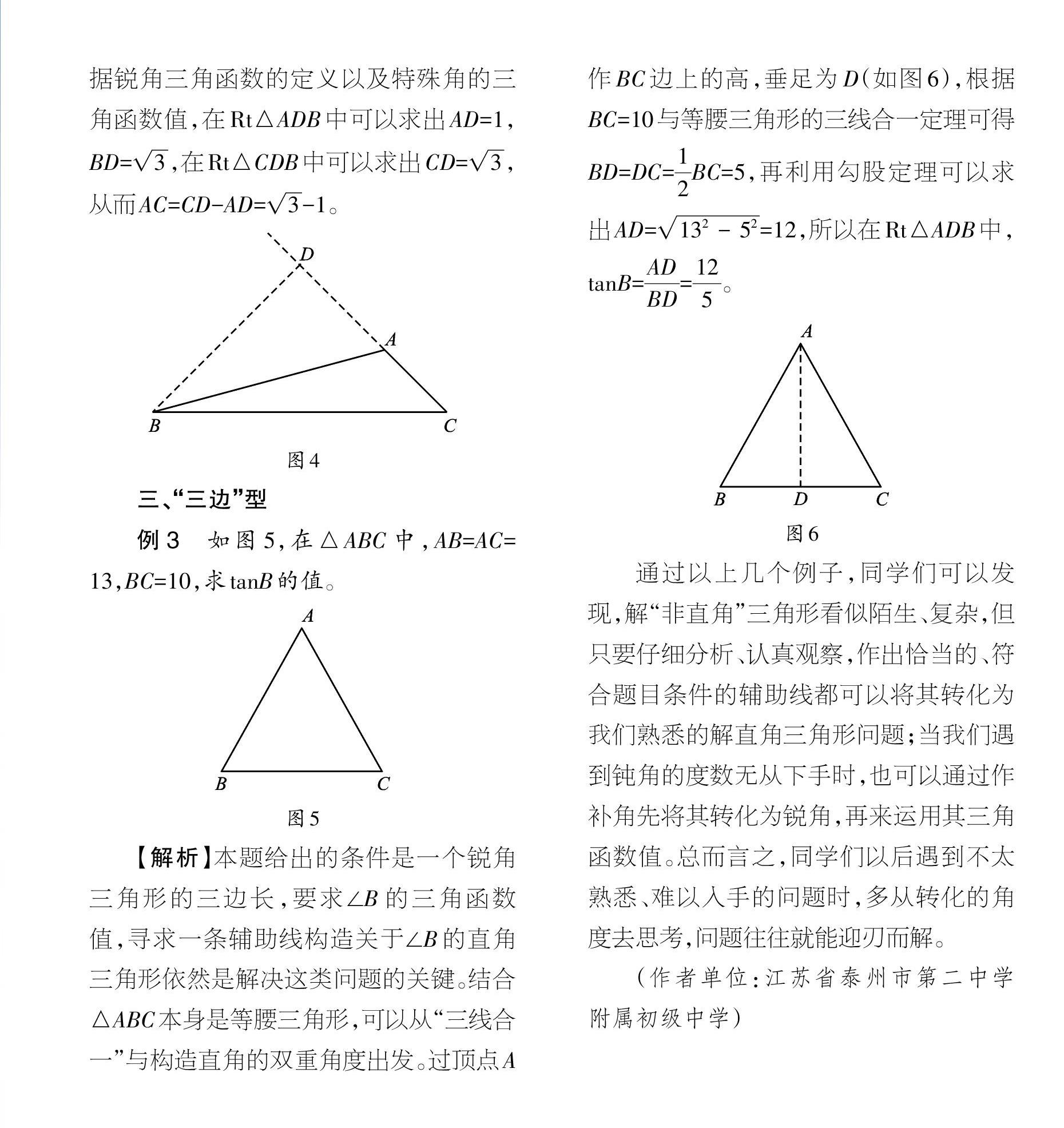



你会解 非直角 三角形吗 参考网



1



70以上三角形3 4 5 角度 シモネタ



直角三角怎么计算角度 西瓜视频搜索



勾股三角形各角的度数 西瓜视频搜索




Opencv 计算三角形的角度 Godlei1995 Csdn博客




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




餘弦定理 维基百科 自由的百科全书



腾讯视频




45度角怎么算斜长 30度角怎么算斜长 星火网校



直角三角形thales定理圆 三角形png剪贴画角度 文本 三角形 平行 免抠素材下载 图片id 1686 其它元素 Png素材 素材宝scbao Com



少有人走的路 三角函数 正弦余弦定理及应用
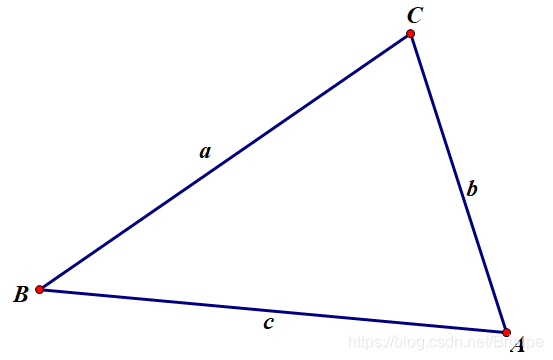



各种三角形边长的计算公式 We Are All In The Gutter But Some Of Us Are Looking At The Stars Csdn博客 三角形边长公式



三角形外角定理 腾讯视频




解三角形距离角度问题应用举例 其实就是换个角度考虑问题 定理 余弦 仰角 俯角 网易订阅



相似三角形 维基百科 自由的百科全书



教育还是严肃些好 希望少些为了博眼球而故意的浮夸 多些实在 腾讯新闻



圆周角定理 弦切角定理 切线长定理 切割线定理证明 哔哩哔哩 Bilibili




枢纽定理 维基百科 自由的百科全书




余弦定理で角度を求める方法 数学の星



莫雷定理 三角形




餘弦定理 维基百科 自由的百科全书



Amc8 金字塔中学等腰等边三角形



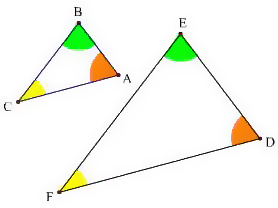
簡要說明常見到的三角形基本性質大致上有 1 與角度有關的等量關係 外角和 內角和 外角定理 2 邊長不等關係 兩邊和大於第三邊 兩邊差小於第三邊
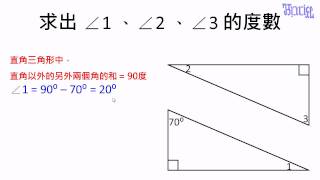



三角形 08 直角三角形內角的基本計算題2 Youtube




例題 三角形角度值含未知數 Youtube



三角形的内角 三角形ppt下载 第一ppt




對頂角 维基百科 自由的百科全书



高中数学牛x 公式 利用三角形关系速解四点共圆题目 努力学习网
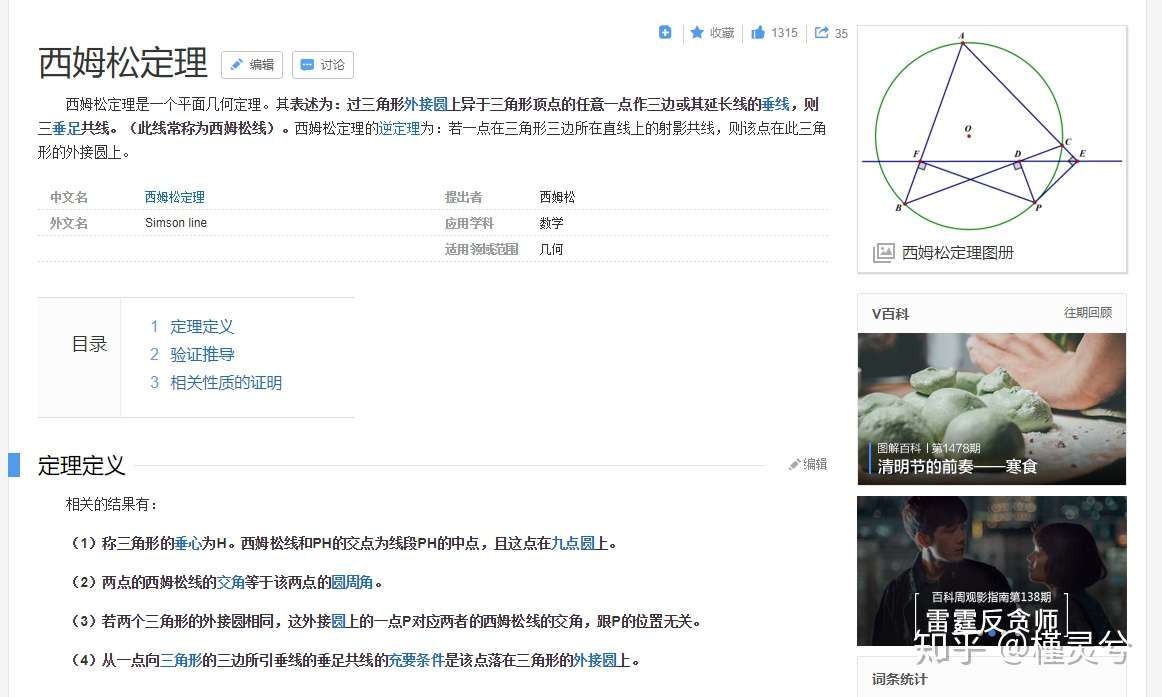



解三角形的新视野 定角对定边 知乎




余弦定理 已知三角形的边求角 几道经典例题讲解 正弦 网易订阅




三角形 维基百科 自由的百科全书



Q Tbn And9gcq1t4a0w Jtwyzsveolshgavsg9w7xikgem6qvqkvmlzjylx9 X Usqp Cau



已知三角形三条边a B C的长度 那么请问该三角形的三个角分别是多少度 秦学教育




如何计算直角三角形的角度 数学21




余弦定理 已知三角形的边求角 几道经典例题讲解 正弦 网易订阅



三角形知道角度求高 西瓜视频搜索




直角三角形知道两边求角度 中考数学专题复习 直角三角形 雪灵谷自然地理的博客 Csdn博客




Hd限定三角形角度問題 最高のカラーリングのアイデア



初中数学几何 梯形辅助线 的做法详解 孩子成绩提升分
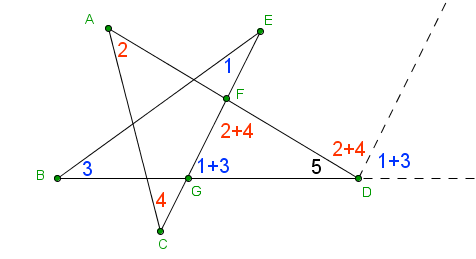



五角星顶点角和为180度的证明 必威app下载
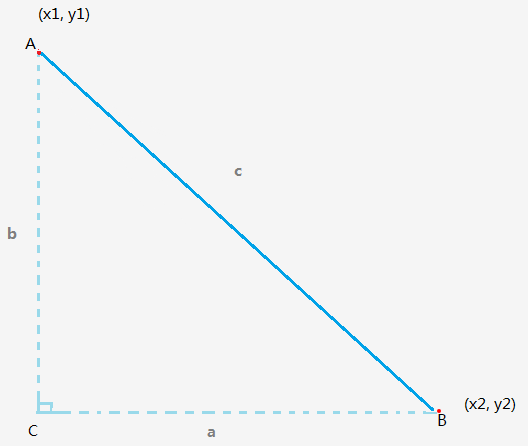



求直角三角形的角度 Front End Math
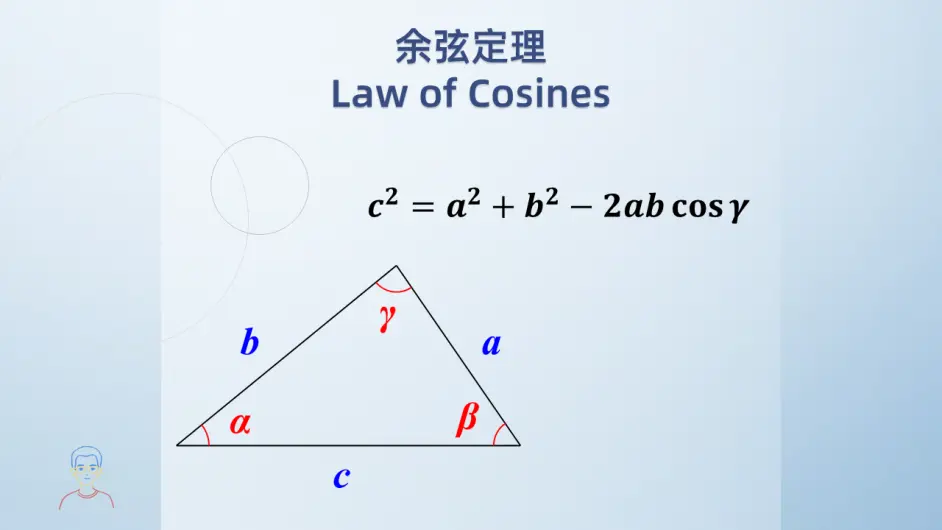



余弦定理 哔哩哔哩
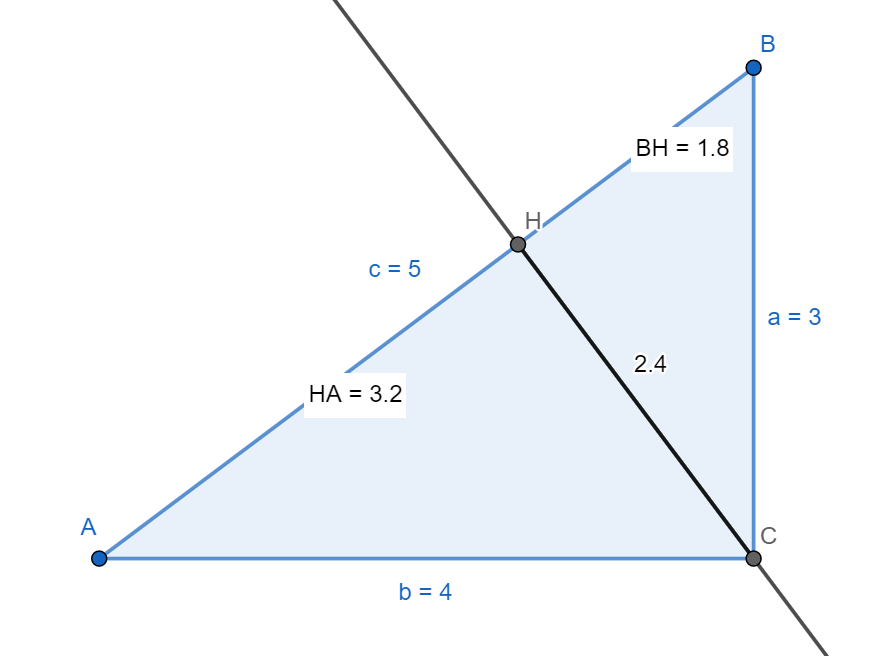



初中 彻底度量345三角形 345三角形的精确角度 精作网




高考数学考点之正 余弦定理及解三角形 王羽课堂




直角三角形面积 周长 夹角 勾股定理 毕达哥拉斯在线计算器 三贝计算网 23bei Com




跟三角形中线 角平分线 高线有关的常见模型和结论总结 每日头条




三角形內角和與外角和定理 Youtube




图形和几何体公式 2 Ai猪的博客
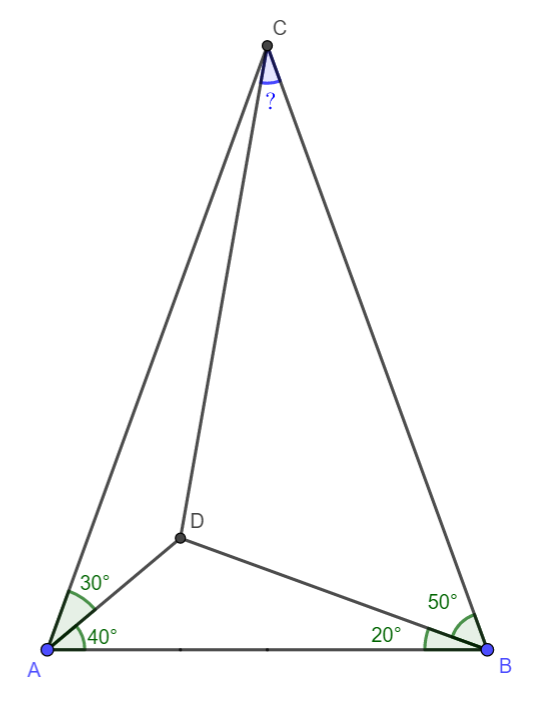



度30度40度50度的角格点几何题 知乎



初中数学 直角三角形中 只给了一个15度和斜边 求直角边长度 哔哩哔哩 Bilibili



直角三角怎么计算角度 西瓜视频搜索



直角三角形毕达哥拉斯定理 三角形png剪贴画角度 矩形 三角形 毕免抠素材下载 图片id 1811 其它元素 Png素材 素材宝scbao Com



勾3 股4 弦5 跟着大何学数学 微信公众号文章阅读 Wemp




余弦定理 已知三角形的边求角 几道经典例题讲解 正弦 网易订阅




角平分线的基础用法 注意角平分线模型 每日头条




等邊對等角 等邊對等角是三角形的一種 在同一三角形中 兩條邊相等 則兩個 百科知識中文網
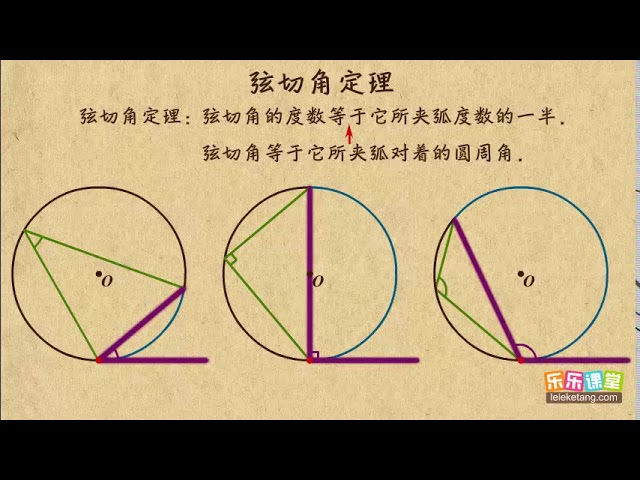



07 弦切角定理 相似三角形的定理与圆幂定理高中数学 Youtube



高中数学牛x 公式 利用三角形关系速解四点共圆题目 努力学习网



四直角三角形的射影定理 人教版高中选修4 1数学电子课本 数九网




相似三角形的性质及其判定定理是什么 星火网校



已知三边求角度 西瓜视频搜索




正弦 余弦定理的应用 测量角度 有关三角形计算




如何找到内角 数学21




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3分钟 搞懂余弦定理 泰勒斯角定理 双偶网
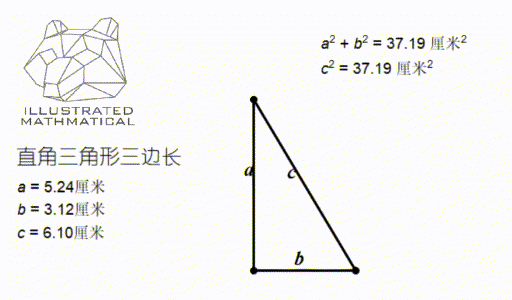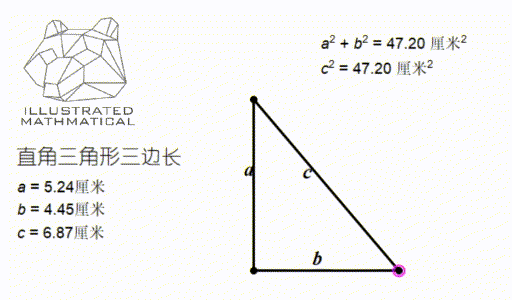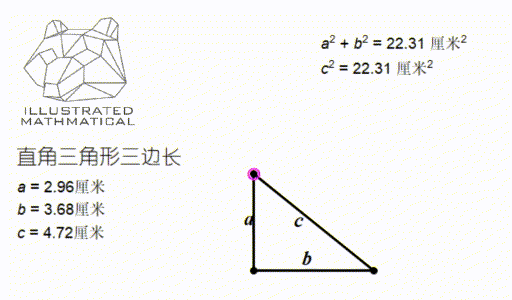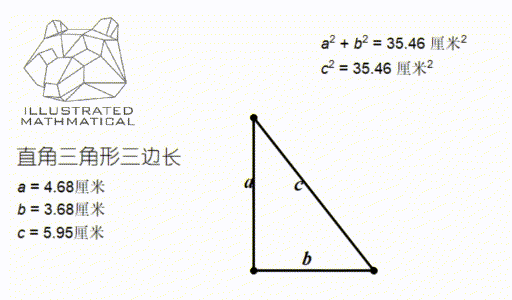



Amc 8 第六讲 直角三角形与勾股定理 知乎




勾股定理怎么算角度




初中篇0 识角度 为什么三角形内角和一定是180 度 而不是100度等 简书



0 件のコメント:
コメントを投稿