√70以上 2 次 方程式 問題 323966

つまり，求めた2次方程式の2つの解が問題 にあてはまるかどうかを確かめる必要がある。 と同時のそのことを文章で表現する必要があ る。 この文章についてはこれといった書き方のき まりがあるわけではない。 その問題ごとに考えて表現すればよい。 たいていはこんな感じ。 「x は××で二次方程式の文章問題（3） ある正の数に5を加えてから2乗すべきところを、間違えて5を加えて2倍してしまったところ本来の答えの6分の1の値となった。このある正の数を求めよ。 「なに間違えてんだよ！」と言いたくなる問題ですよね。 これも二次方程式の文章題では頻出です。 難しい数学2次方程式 一覧 HOME 数学プリント スポンサーサイト iドリル iドリルは、中学生向けの完全無料問題を配布している学習サイトです。掲載されいている学習教材は実際に学習塾でも使用している教材で、数学・英語・理科・社会の問題のほか、入試対策問題も配布しています。 i

求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博

2 次 方程式 問題

2 次 方程式 問題-中学数学定期テスト対策 中3分野「平方根」を以下のように訂正しました。 解答③素因数分解と平方数の大問4の解の部分。 また、解答の訂正に伴い解説も訂正しております。 定期テスト数学対策 中1分野 「文字と式」を以下のように 今回は、前回より難しい2次方程式の解き方を見ていく このレベルまでできれば、十分ではある。 前回 2次方程式の解き方と練習問題(1)(基) 次回 2次方程式の解き方(3)(難) 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二乗

一元二次方程的實際應用 常見應用題的解題方法及步驟 每日頭條

2次方程式の実数解の個数（判別式）の練習問題 解答 練習問題 解答 （1） ① 判別式を利用する。 （ ， ， ） 判別式を とすると， 計算して， となるので，実数解の個数は2個 ②19/8/28 3年 2次方程式総合問題Lv3 3(2)図の記号が間違っていました。 19/8/9 3年 1,2年の復習Lv1 2② xの値が2から6まで(誤)→xの値が1から6まで(正) 19/7/29 3年 2乗に比例する関数 変化の割合Lv3 1⑤問題 1/6→1/6, 2(2)答 6→ 72 19/5/8 2年 式の計算総合問題1 2①と②の解答が逆になっていました。4の答が 解の公式を使った2次方程式の問題 次は、以下の問題を考えてみるかのぉ \( 2次方程式 x^25x3=0 を解いてください \) ではまず、解の公式を使うために、a, b, c の値を決めるかのぉ \( x^25x3=0 \) と \( ax^2bxc=0 \) の各項を比べると、 \( a = 1, b = 5, = 3 \) となるわけじゃ 数学おじさん bとcは

中2 数学1次関数の問題（1）問題と解説 方程式の解き方・等式の性質問題と解き方 中学2年生の数学1次関数の基本問題プリント問題と解説 まだ間違った勉強法で苦労し続けますか？ 中学生の数学│難問空間図形の難しい問題（22次方程式の解き方について解説していきましたが、今回は2次方程式の文章題などの応用問題の解き方についてです。 解き方自体は1次方程式や連立方程式とほぼ同じ。 文字で関係式を作り、それを解いていくという感じです。 2次方程式の文章問題を解くこんな問題です。 「難しそう」と思った方が多いと思います。 しかし、 接線の求め方はやり方を覚えたら大したことないです。 本記事では 2次関数の接線の求め方を解説 します。 この記事を参考にして、接線を求められるようにしましょう。

今回の問題は図形の知識も必要となる2次関数（$ y＝ax^2 $）の問題ですね。 （1）と（2）は本当に基礎・基本の問題になっています。 もし、（1）と（2）の問題を解くのに時間がかかったり、迷ったりする場合は、基本問題を中心に解き直し、シッカリ理解しておきましょう！ （3）は複合問題に2次方程式の解の配置問題の解き方 グラフを書いて ( y y 軸は書かない)，3つの条件 ・端点条件 (端点の y y 座標を図から判断) ・軸条件 (軸の範囲を図から判断) ・判別式 ( D > 0 D > 0 か D ≧ 0 D ≧ 0 か判断．頂点の y y 座標で判断してもOK．) をチェック．これ数学33章二次方程式「二次方程式の利用」＜準備問題①＞ 組 番 名前 次の方程式を解きなさい。 (1)3χ2－15＝0 (2)(χ＋7)2－18＝0 (3)χ 2＋10χ＋24＝0 (4)χ－12χ＋35＝0 (5)χ 2－χ－72＝0 (6)χ＋19χ＝0 (7)χ2－18χ＋81＝0 (8)3χ2＋9χ＋2＝0 (9)χ 2－3χ＋1＝0 (10)χ－6χ＋2＝0 5 2 57 5 7 5 18 32 2 6 2 2 2 2 2 数�

中学３年生 数学 ２次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

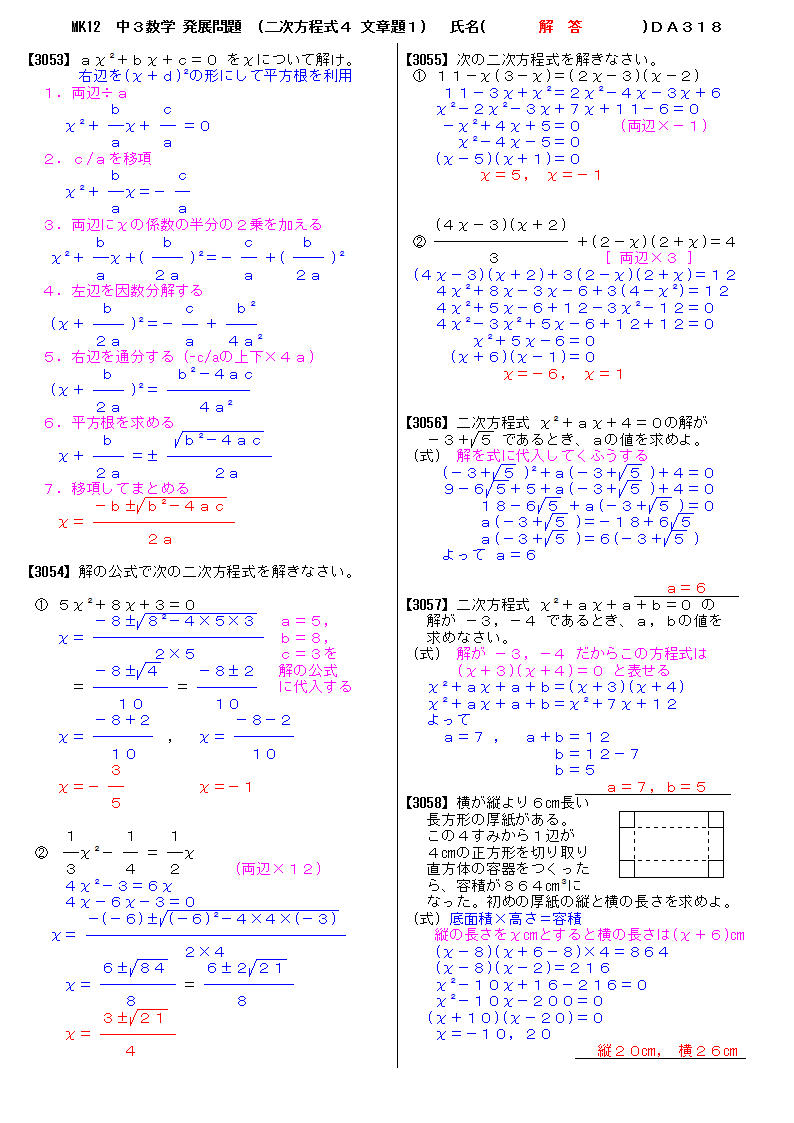
無料 中３数学 発展 応用問題 解答プリント 318 ２次方程式４ 文章問題１

 速度と距離の問題（1次方程式） 投稿日 年2月12日 年12月8日 100sai 方程式を利用して問題を解くときには、問題文の中のどれかひとつの量を\(~x~\)として、他の量を\(~x~\)を使って表し、それらの量の関係を満たす方程式をつくります。 食塩水の濃度の問題（2次方程式） By 100sai 年5月19日 年12月12日 2次方程式の利用 食塩水と濃度（濃さ）の関係は次のようになります。 食塩水の重さ= 食塩の重さ 水の重さ 食塩水の濃度 (%)=食塩の重さ 食塩水の重さ 食塩の重さ＝ 食塩水の まず、古代バビロニアの2次方程式に関する問題を見てみましょう。 "例えばスーサ出土の問題集（TMS,No6）に, 「正方形の面積から,一辺の長さの4倍が引かれて780一辺の長さはいくらか？;問題21」 という問題があり（後略）" （引用元：中村 滋,室井 和男「数学史 ―数学5000年の歩

一道计算一元二次方程解的算法题 Sesiria的博客 Csdn博客 一元二次方程算法

三元二次方程 三元二次方程是指有三個未知數 最高次數為二次的方程 一般 百科知識中文網

二次方程式問題の解説付き！解き方をパターン別に説明していくよ！ スマホでご覧いただく場合、数式が長すぎて画面に表示しきれない場合があります。 その場合には、数式を横にスライドしていただくことで式の続きを表示していただけます。 Contents 二次方程式の難問に挑戦！ 中3方程式では3m、30mと2つの答えが出てきましたが 問題のシチュエーション的に30mの道幅はありえないから 今回の問題の答えは 3m となります。 二次方程式の文章問題では このように問題のシチュエーションに合っているか確かめることが大切です！ 2次方程式の利用の動点に関する問題です。 ある点が時間が経つにつれて移動する問題で、 移動する距離をx とおいて、必要な辺の長さなどをxの文字式でおき、面積などの方程式を作っていきます。 テストでもよく出題されますので、しっかり出来るようにしておきましょう。

配方法頂點

一元二次方程式

 今回から、2次方程式を見ていく。 まずは、2次方程式の解き方から始めよう。 前回 ←平方根の補充問題(難) 次回 →2次方程式の解き方(2)(展開、置き換え、二乗の利用)(標) 31 2次方程式の解き方 311 基本的な2次方程式の解き方(1)(基) 312 2次方程式のの解き方(2)(展開・置き換え・二2次方程式の解の公式（虚数解含む） 3次方程式 フリ－ソフトwxMaximaによる高次,連立方程式の解き方 二次方程式の解の公式 解説 （問題は下にあります．） x 2= a の解は x = ± √ a √ni です． （中学校では， a は 0 以上とします．） その応用として2次方程式の解と係数における関係式なので，そのまま"解と係数の関係"という公式名になっています． $\alpha\beta$ と $\alpha\beta$ が基本対称式になっているので，何かと登場機会が多く，暗記必須の公式です． 以下に示す証明を理解しておくと，忘れてもその場で導けます．

2次方程式の利用 整数 自然数 教遊者

例題 一元二次應用題 果園面積 Youtube

第3章 二次方程式 ＜前： 『第2章 平方根』の復習テスト の問題 L17 二次方程式の基本と解 の解答 ：次＞ 練習問題1 以下の（ア）～（カ）の方程式の中から二次方程式であるものを選び、記号で答えなさい。 （ア） x 2 ＝13 （イ） x 2 ＋3 x ＋2＝0数学Ⅰ「数と式」「2次関数」で使う公式をpdf（a4）にまとめました。 演習の際にご活用ください。 公式 8 絶対値の問題一覧 数学Ⅰ「絶対値」の教科書の問題と解答をプリントにまとめています。 教科書の問題は出版社によって異なりますが、主要な教科書に目を通し、すべての問題を網羅基本的に中学校で出題される2次方程式の問題はすべて平方完成で解くことができます。 ただ、因数分解できる2次方程式は因数分解で解く方が簡単なので、因数分解できない問題を平方完成するのが基本となります。 平方完成を利用した2次方程式の解き方 今回は例題として \(x^24x6=0\) を平方

2次方程式 2 どの方法で解けばいいの バカでもわかる 中学数学

二次方程式で解の公式を使う問題 見分け方は因数分解がポイント 中学や高校の数学の計算問題

2次方程式の整数解問題 実践例題③1 例題3 解答 2次方程式x2 (a1)x3a 1= 0 が整数解を少なくとも1つもつとき, 整数 a の値を求めよ。 2次方程式の整数解問題は,まずは,判別式 D≧0 より,範囲が絞れないか試してみるが,この場合 絞れない。そこで,文字(整数)に短辺と長辺の比が, 長辺から短辺を引いた差と短辺の比に等しいような長方形を「黄金長方形」(golden rectangle)と呼び, その辺の長さの比 $1\dfrac{1\sqrt 5}{2}$ (約 $35$)を「黄金比」(golden ratio)と呼ぶ「黄金比」は最も美しい比であると言われ, 多くの美術作品の中にこの比を見ることがで 2次方程式・2次不等式の特訓プリントです(`・ω・´) この2つは数学の最重要単元の一つなので、必ず解けるようにしておきましょう！ 因数分解、解の公式を完璧にしておきましょう(*´ω`*) 2次方程式 ＜2次方程式＞ 数学Ⅰ 2次方程式特訓① 問題編

09增长率问题一元二次方程初中数学初三 Youtube

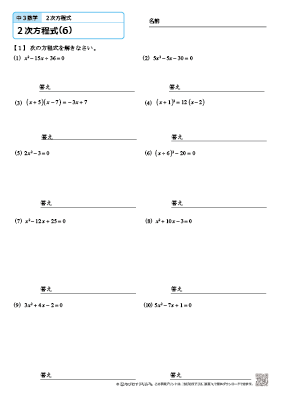
中学３年生 数学 ２次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

 数学の問題です。 2次方程式x^22mx4m=0が次の条件を満たすように、定数mの値の範囲を定めよ。 (1)異なる2つの実数解をもつ (2)実数解をもたない よろしくお願いします。 数学 高次方程式の解の問題で、 複素数1iが四次方程式x^4ax^37x^2bx26=0の解であるとき、実数の定数a,bの値はいくつか また2次方程式 (x2) (x−2)=2 (3x−2) を解きなさい。 両辺に式があるような二次方程式は，展開・整理して式を左辺に集めてから考えます． 前問と同様に， x=0 を忘れないように気を付けましょう． 方程式 x 2 −2x−35=0 を解きなさい。 左辺が因数分解できる二次

基測數學 98v2 單選34 一元二次方程式的應用問題 評量專區 均一教育平台

中学1年生 数学 無料問題集 一次方程式 おかわりドリル

二元二次方程解法 哔哩哔哩 つロ干杯 Bilibili

一元二次方程的应用题 十五种必考题型总结

初中数学一元二次方程求根公式 一元二次方程的解法 一元二次方程根与系数的关系 101教育知识点频道手机端

2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学

解一元二次方程式之應用問題合理性 Live 多媒體數學觀念典online

北师大版九年级数学上思维特训 七 含答案 一元二次方程根与系数关系的运用技巧 七七文库www 77wenku Com

解一元二次方程十字相乘法专项练习题 知乎

九年级数学一元二次方程专项测试卷附详细答案 每日头条

2

中3数学 2次方程式の利用 図形に関する問題

例題 利用配方法解一元二次方程式2 二次項係數不為1 數學 均一教育平台

2 2用配方法求解较复杂的一元二次方程 第2课时 课件 七七文库www 77wenku Com

一道计算一元二次方程解的算法题 Sesiria的博客 Csdn博客 一元二次方程算法

初中數學 一元二次方程的常見考點 你都掌握了哪些 每日頭條

二元二次方程式圖形

基本数学 3秒で暗算したい普通の2次方程式 暇つぶしに動画で脳トレ

２次方程式の文章題ー図形の問題 無料で使える中学学習プリント

二次方程式公式解一元二次方程 Ejthgg

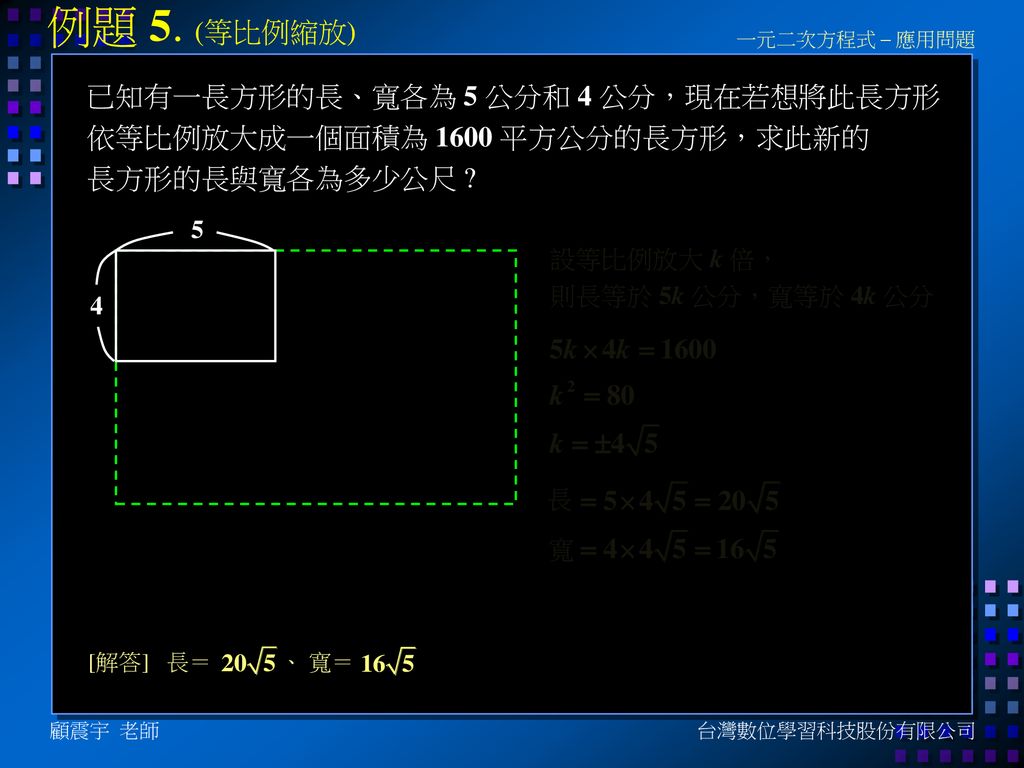
一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download

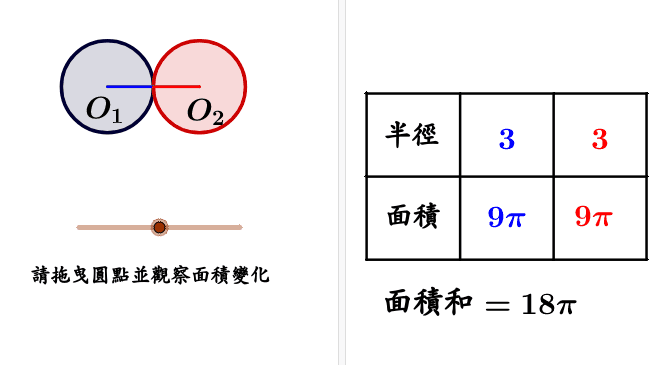
一元二次方程式 應用問題 兩圓相切 3 Geogebra

一元二次不等式題目鍾老師教學網 Qhcoh

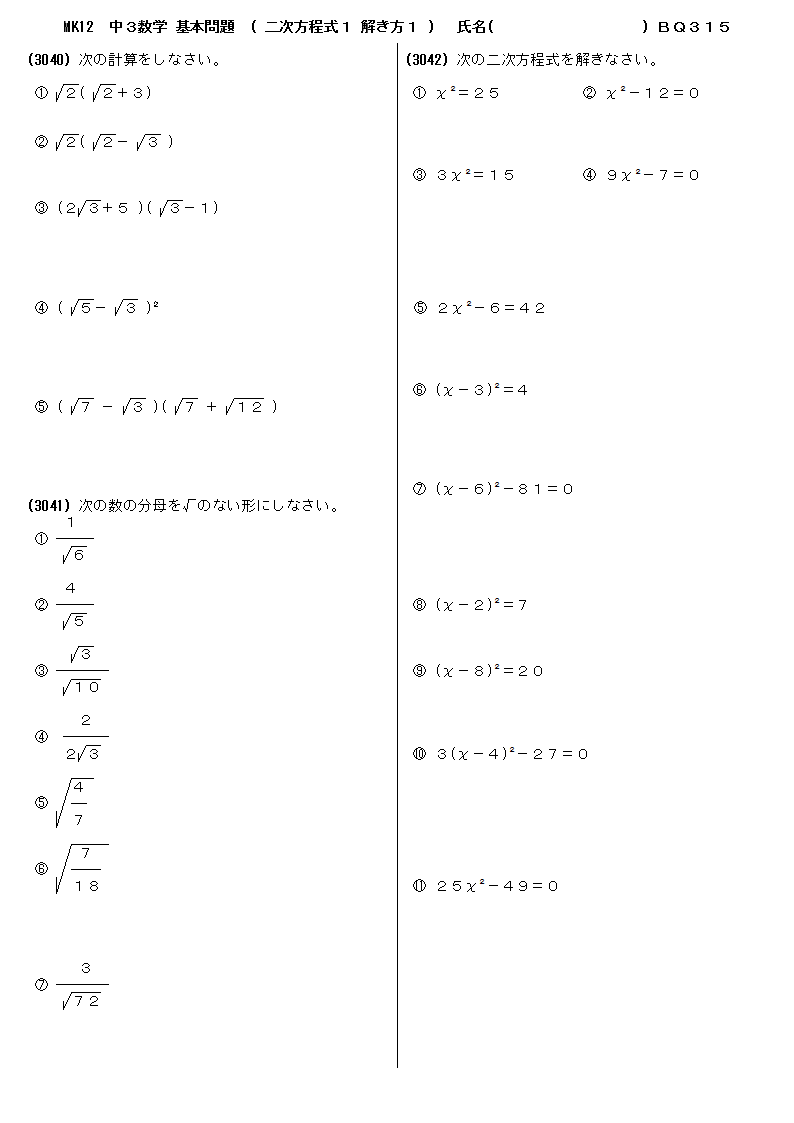
0以上2 次方程式問題 シモネタ

求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博

23 2 一元二次方程的解法 5 修订版教案 Rar 华九上 22 2一元二次方程 的解法 初中华师大版13版 数学中国网 Mathschina Com

二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは５つ 中学や高校の数学の計算問題

一元二次方程的實際應用 常見應用題的解題方法及步驟 每日頭條

二次方程式の利用 面積 Youtube

一元二次方程式應用問題 例4 5 6 均一教育平台

2次方程式 数学入試問題

應用問題4 一元二次方程式 發現學習的美麗新世界

中学数学 二次方程式

中学数学単元別 2次方程式 数学中学校教材問題集 Buyee 日本代购平台 产品购物网站大全 Buyee一站式代购bot Online

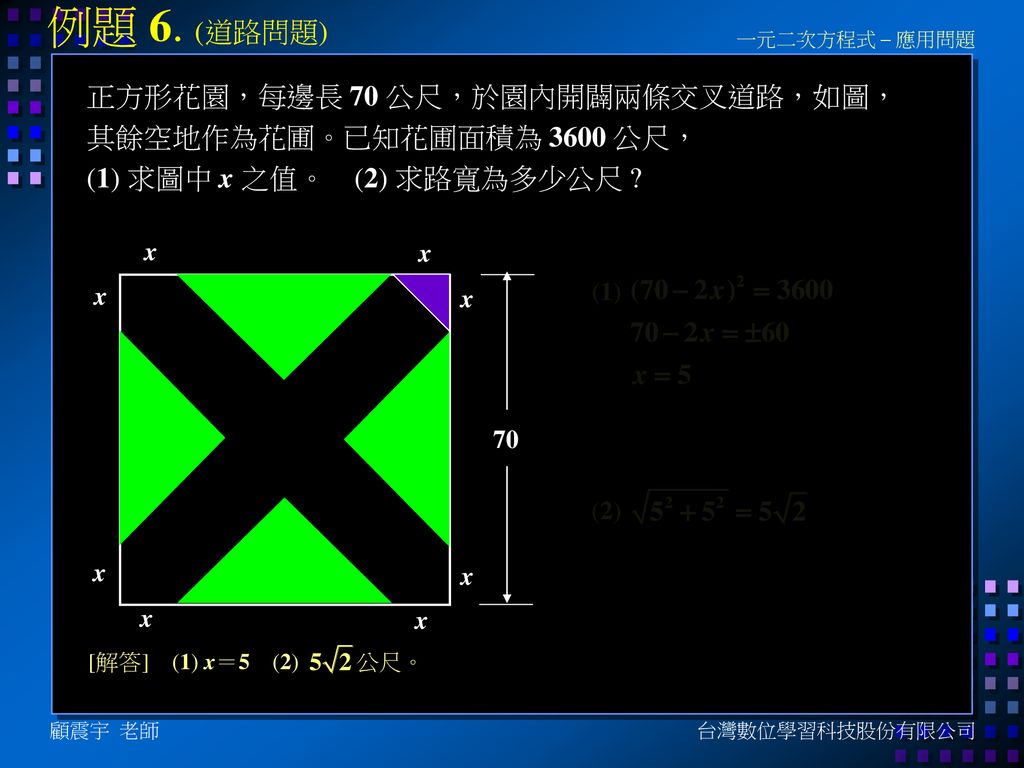
一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download

世界一わかりやすい数学問題集中３ ３章 二次方程式

中学３年生 数学 ２次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

配方法解一元二次方程方程解法 哔哩哔哩 つロ干杯 Bilibili

解一元二次方程式 明誠中學程式設計學習網

二次方程式の利用 チーム エン

最良かつ最も包括的な中1 方程式問題 ぬりえ壁紙hd

高校入試 二次方程式の難問を解説 難関高校の入試問題に挑戦 数スタ

19九年级数学上册第二章一元二次方程2 用配方法求解一元二次方程 第2课时 教案

1 次方程式問題 シモネタ

一元二次方程 面积类应用题 4种重要题型详细分析

2

二元二次方程式配方法二元二次方程組的解法 初三網 Tuguht

九年級數學一元二次方程應用題專項練習 帶答案 每日頭條

毎日計算練習問題 ２次方程式でb の解の公式を使う 彦根市の高校数学専門個別指導学習塾 安澤数学教室

二次方程式の利用 文章問題 解き方まとめ 方程式の解き方まとめサイト

1

一元二次方程式 备课吧

名師課輔網 數學一元二次方程式的應用

最も欲しかった 数学2 次方程式 ニスヌーピー壁紙

世界一わかりやすい数学問題集中３ ３章 二次方程式

这几类一元二次方程应用题不会 中考考高分难了 热点题 楠木轩

一元二次方程配方法 4道提高题 全做对你就是学霸水平 初中 Qq教育网

一元二次方程式應用問題 例4 5 6 Youtube

二次方程式の利用 スタディーx

２次方程式ーいろいろな計算 無料で使える中学学習プリント

8年級上數學 資優題 一元二次方程式應用問題 17 12 30 Youtube

中３数学 二次方程式の解き方と因数分解 解の公式の覚え方と簡単な計算問題 猫に数学

中学３年生がぎりぎり解ける一番難しい ２次方程式を教えてください Yahoo 知恵袋

Learnmode 學習吧

求解一元二次方程式不再繁琐 美国数学博士发现简便新方法 罗博

問題 數學問題一元二次方程式 校園生活哈啦板 巴哈姆特

十字交乘part Vscizr

亿源老师教案发表 配方法解一元二次方程式 备课吧

109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass

二次方程式 置き換えを利用する チーム エン

一元二次方程應用題總結分類及經典例題 每日頭條

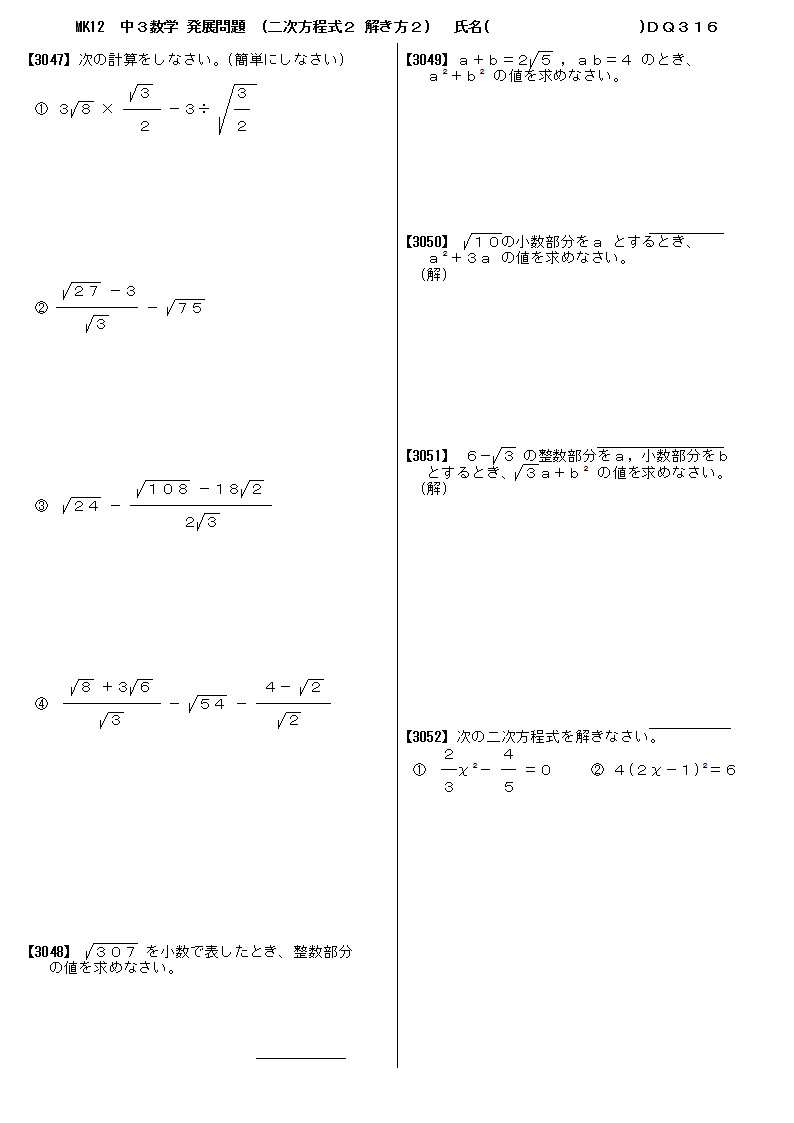
無料 中３数学 発展 応用問題 問題プリント 316 ２次方程式２ 解き方２

一元二次方程式 應用問題 顧震宇台灣數位學習科技股份有限公司 Ppt Download

隨筆誌 二上4 1因式分解解一元二次方程式 看錯係數解正確解相關問題

二次方程式の解き方 平方根の知識を使う問題のパターン 中学や高校の数学の計算問題

二次方程式の解がわかっている問題は ｘに代入して計算しよう 中学や高校の数学の計算問題

一元二次方程式應用問題 例3 Youtube

中考數學 一元二次方程的根與係數的關係與代數式的恆等變形 每日頭條

愛學網播放影片

２次方程式の解と係数の決定 無料で使える中学学習プリント

2次方程式の解き方 解の公式を利用 数学fun

dce D0d2 4af9 9861 1f16f8f518 Filesusr Com

韦达定理 一元二次方程根与系数的关系 新华网

109 數學基礎自學講義八年級 一元二次方程式的應用問題 第三冊4 3 Shareclass

中学３年数学 二次方程式 解の公式 確認問題２ あんのん塾

中考 一元二次方程解應用題 題型總結 轉給需要的同學吧 壹讀

年中考数学必考考点 一元二次方程及其应用 初中数学知识点概念大全练习题 哔哩哔哩

2次方程式の解の配置問題 おいしい数学

中3 数学 二次方程式の利用 中学生 数学のノート Clearnote

二次方程式の問題を教えて下さい Clearnote

Learnmode 學習吧

中学３年生 数学 ２次方程式の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生