
文字式の利用 連続する3つの整数の和が3の倍数になる証明 Qikeru 学びを楽しくわかりやすく
ヒント・考え方 一般に, 2 2 つの集合 X,Y X, Y が一致することを示すには, X ⊆ Y X ⊆ Y と Y ⊆ X Y ⊆ X をそれぞれ示すのが常套手段です. →集合の相等の証明 つまり,今回の場合 連続する10個の自然数の和とは、例えば とか のようなものです。上の和は55ですし、下の和は715です。 こんな計算が、あっという間にできるというのがテレビでやってたんです。
連続する整数の和 証明
連続する整数の和 証明- にほんブログ村 1は1個だけなので連続していないということになります。) それに対して、「連続する整数の和」で表すのは、1以外の奇数の約数の個数だけ式が出来るので、上記の式 1から までの自然数の和は、次のように求められる。 1 2 3 ⋯ n = 1 2 n ( n 1) 例えば、1から100までの和であれば、 1 2 × 100 × ( 100 1) = 5050 と求められます。 直接足す

問題 連続整数の積の和の計算 ハイスピード数学プロブレム002 とぽろじい 大人の数学自由研究
15から始まる1つの連続する整数の和 1から始まる5つの連続する整数の和 4から始まる3つの連続する整数の和 7から始まる2つの連続する整数の和 の4通りで表されることか連続自然数の個数が1つ増えるたび,右辺の分母が1つ大きくなり,かける項も増えます. ちなみに $\displaystyle \sum_{k=1}^{n}k=\frac{1}{2}n(n1)$ は連続自然数積の和ではありませんが,同じ規2つの続いた数をn、n+1とします。 そうすると、この2つをたすと、 n+(n+1)=2n+1となりますよね。 整数を二倍した数は偶数であり、偶数に1を足した数は奇数となるのでよって、連続し
2のベキ(2^n)でない数は「2つ以上の連続する自然数」(必ずしも1から始まる必要はない)の和で書けること (2) 2のベキ(2^n)で書ける数は完全数ではない。 (1)の証明 2のベキ(2^n)でない 自然数を 2 個以上の連続する自然数の和で表すことを考える。たとえば,42 は $34\cdots9$ のように 2 個以上の連続する自然数の和で表せる。次の問いに答えよ。 (1) 連続する~ の大まかなパターン 連続する整数は前回の記事でも説明した通り、 1,2,3,4,5,6,7 と1づつ増えていく数列上の数のことを言いました。 まず1つ覚えていた
連続する整数の和 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
整数の和 | 整数の和 | 整数の和 |
 整数の和 | 整数の和 | 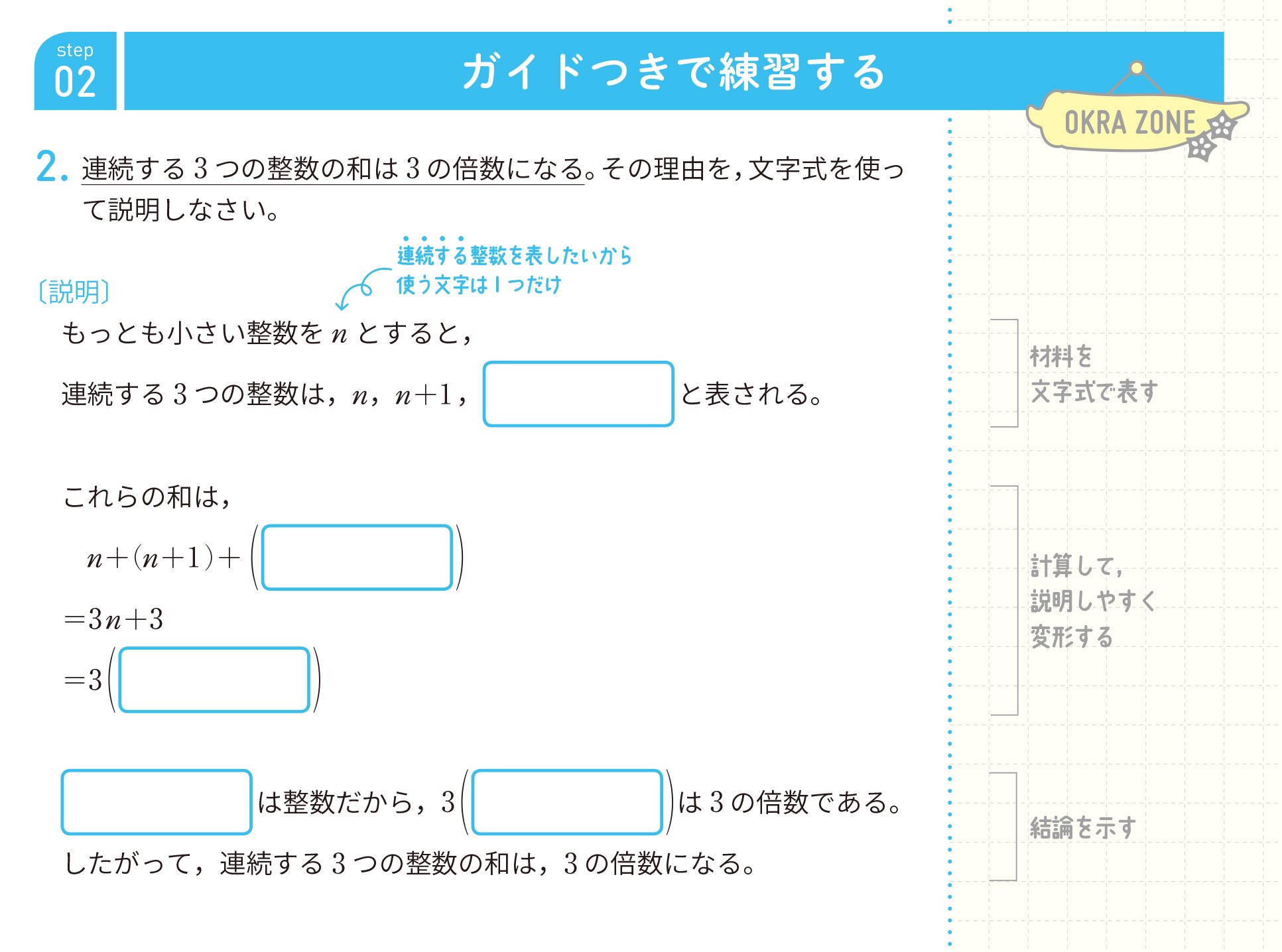 整数の和 |
 整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 | 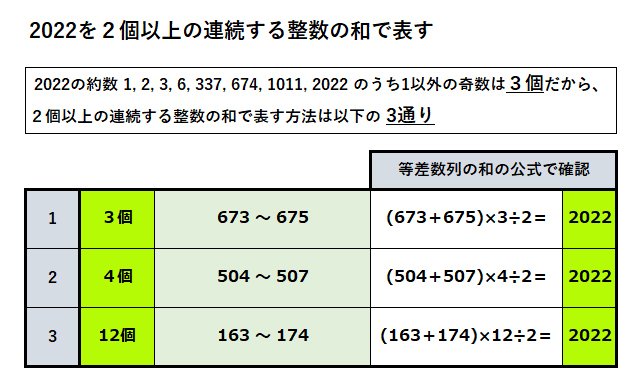 整数の和 | 整数の和 |
 整数の和 |  整数の和 | 整数の和 |
整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
整数の和 |  整数の和 |  整数の和 |
 整数の和 |  整数の和 |  整数の和 |
整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
整数の和 |  整数の和 |  整数の和 |
 整数の和 |  整数の和 |  整数の和 |
 整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 | 整数の和 |  整数の和 |
 整数の和 | 整数の和 |  整数の和 |
 整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 | 整数の和 |  整数の和 |
整数の和 | 整数の和 | 整数の和 |
 整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 | 整数の和 |  整数の和 |
 整数の和 | 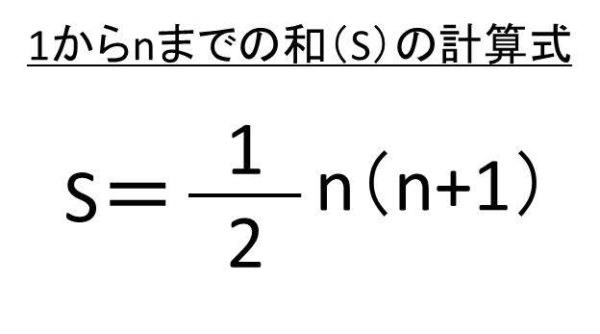 整数の和 | 整数の和 |
整数の和 |  整数の和 | 整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 | 整数の和 |  整数の和 |
 整数の和 |  整数の和 |  整数の和 |
整数の和 | 整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 |  整数の和 |  整数の和 |
整数の和 |  整数の和 | 整数の和 |
 整数の和 |  整数の和 | 整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
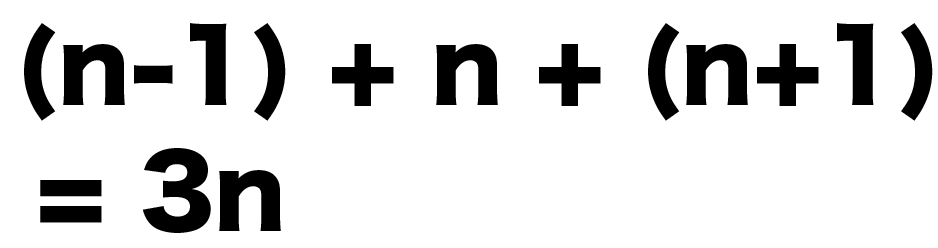 整数の和 | 整数の和 | 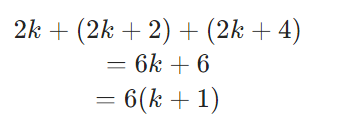 整数の和 |
 整数の和 |  整数の和 |  整数の和 |
整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 |  整数の和 |  整数の和 |
 整数の和 | 整数の和 |  整数の和 |
 整数の和 |  整数の和 |  整数の和 |
「連続する整数の和 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の和 | 整数の和 |  整数の和 |
 整数の和 |  整数の和 |
を消去すると, 偶数個の自然数の和が残る。 予想 8N が奇数個の連続する(必ずしも正で はない)数の和として表現可能なら, Nは奇 数の約数を持つ。 32 「連続する自然数の和の問題」の複数の証 明 連続する5つの整数の和は たとえば 1つの場合として 1+2+3+4+5=15となり 15=5x3なので 5を3倍すると15になるので 5の倍数であることがわかります 5つの組み合わせす
Incoming Term: 連続する整数の和, 連続する整数の和 公式, 連続する整数の和 証明, 連続する整数の和 中学受験, 連続する整数の和 方程式, 連続する整数の和で表す,




0 件のコメント:
コメントを投稿