ベストアンサー:分数は比ではなく割合(比率)を表しているので 比が1:1だとすると 片方の割合は (比の数) /(全体の数) 1/ (11) 1 1745 検索結果をもっと見る( 3,091 件黄金比は様々な場面で登場します,まずは最も重要な性質を紹介します。 性質1 黄金比は方程式 x 2 − x − 1 = 0 x^2x1=0 x2 −x− 1 = 0 の解である。 性質1は二次方程式を実際に解くことで簡単に確認できます。 黄金比の定義と見ることもできます。 数学 (2) 比の値を利用して解く。 (3) 比が割合であり、分数にも置き換えられることがわかっていれば良いか。 3. なぜ、内項の積と外項の積は等しいのか。 4. 結局は同じ計算をしているということがわかれば。

分数 Wikipedia
比の性質 分数
比の性質 分数-A^0=1 a0 = 1 であることから直接分かる,この方が素直) なお,6については 底の変換公式の証明と例題 で詳しく解説しています。 1~6を使えばほとんどの対数の計算問題を突破できますが, 覚えておくと便利な対数の公式3点セット を使えばさらに見通し まずは「比例式の性質」について、説明していきましょう! 比"1 3″と比"3 9″を例に、考えてみたいと思います。 比"3 9″は両方の数を3で割れば、"1 3″になりますね。 よって、比"1 3″と比"3 9″は等しいことになります。 つまり、



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html
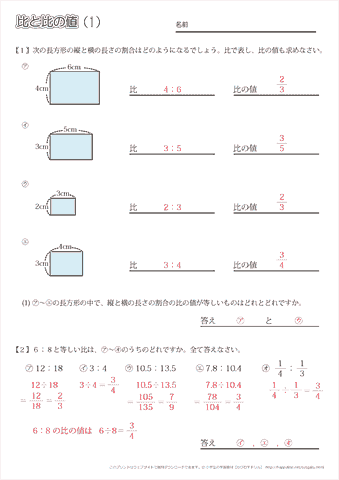
分数の倍とかけ算・わり算(1) 分数の倍とかけ算・わり算(2) 力をつけよう 5 対称な形 線対称 問題一括 (2,770Kb) 解答一括 (2,7Kb) 点対称 多角形と対象 力をつけよう 6 比と比の値 割合の表し方 問題一括 (2,807Kb) 解答一括 (4,178Kb) 等しい比 簡単な比 比の 分数 分数の性質 加比の理二つの分数が等しい場合 b a = d c ( b × c = a × d ) {\displaystyle {b \over a}={d \over cフィボナッチ数列と黄金比 もっと数学の世界⑦(中学生以上) フィボナッチ数列 今回はある有名な数列の紹介からはじまります。 次の数列はどのような規則にしたがって数がならんでいるでしょう。
「比の値」の用語とその意味,求め方を理解する。また,比の値を求めて等しい比を見つける。 比の性質を理解し,等しい比をつくる。 比の性質を使って,比を簡単にする方法を理解する。 小数や分数で表された比を簡単な整数の比になおす方法を理解する。図形と計量180°θの三角比 図形と計量90°θの三角比 図形と計量90°以上の角の三角比の値について 図形と計量cosの値が負になるときの角度の求め方 図形と計量sinを含む分数の式の計算方法 図形と計量sin,cos,tanの値の覚え方ちなみに比の基本や文章問題の解き方などはこちらに詳しく説明しています。 比の性質と問題の解き方|小学生に教えるための分かりやすい解説 「砂糖と塩を\(1:2\)の割合で加える」「勝敗は\(3:2\)で勝ち越している」「縮尺は\(1:5000\)」 このように
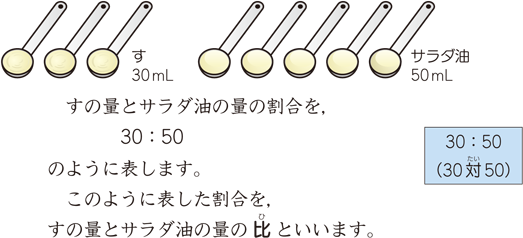
小数・分数になると等分除で説明するには 限界がある。第一用法では,除数が整数・ 小数・分数のいずれでも説明が可能である。 次に,分数の除法になる問題にはどのよ うな問題があるのかを考え,問題を分類化 していきたい。 4 これを算数の「比」を使って表すと 「カフェオレ」の 「コーヒ:牛乳=7:3」 「:」は「対(たい)」と読みます 「比」とは「割合」を表す1つの方法です 「7:3」は「7対(たい)3」と 読んでください ここでは 「比」の性質や使い方について 見ていき比は、その比に同じ数を掛けるか割った別の比と同じという性質を持っています。 12 = 24(左の比に2を掛けたのが右の比) 36 = 12(左の比を3で割ったのが右の比) 比の関係は分数の関係によくに




分数のかけ算の計算プリント 帯分数編 全240問無料 算数パラダイス




分数の比を簡単にする 問題の考え方を図解で説明します 算数 数学 の文章題 特殊算など のことを書くページ
比例式 比は、小学生のときにも見ましたが、\ 12 \などと表されるものですね。例えば、「 x と y の値は $12$ だ」といえば、「 y を基準にしたときの x の割合は、 $2$ を基準にしたときの $1$ の割合(=05)と等しい」という意味で、簡単に言えば、「 y は x の2倍 」という意味にななお,線分を黄金比で分けることを,黄金分割 (Golden Section)という. 7.おわりに 今回は,黄金比の定義や基本的な性質について言 及したが,フィボナッチ数列との関係等,黄金比に は,他にも面白い性質が沢山ある.また,黄金比は になるね。だから比例式の性質、 が成り立つんだね。 そして、 比例式の性質はあたかも「比の外側同士」「比の内側同士」の項をかけてるようにみえるよね?? だから、ちまたでは「比例式の性質」のことを、 外項の積・内項の積 って呼ぶことがあるん




帯分数の足し算の計算プリント 分母が同じ問題 全240問無料 算数パラダイス
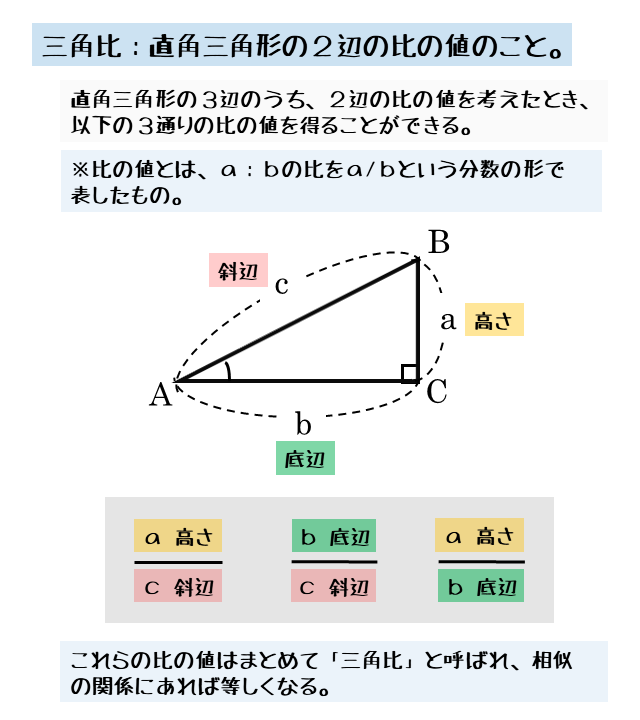



図形と計量 三角比の定義について 日々是鍛錬 ひびこれたんれん
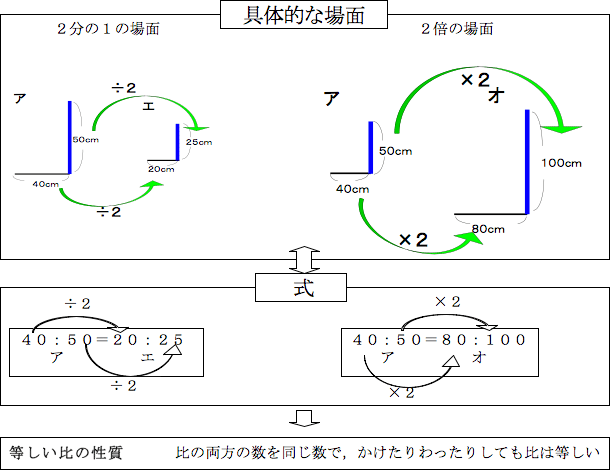
平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので比には,次のような性質があります。 1 A:B= (A×C): (B×C) Cは0以外の数 2 A:B= (A÷C): (B÷C) Cは0以外の数 比を,それと等しい比で,できるだけ小さい整数の比になおすことを比を簡単にするといいます。 ・比例配分 ある量をきめられた比に分けること表さないこと。比の値は、分数、 小数、整数でも表されること。 考比の値における比べる量と もとにする量の関係 4 「等しい比」 ・比が等しいことの意味 や等しい比の性質がわ かり、それを使って、等 しい比を見つけることが できる。 比が等しい




比と比の値 その2 家庭学習レシピ




分数 Wikipedia
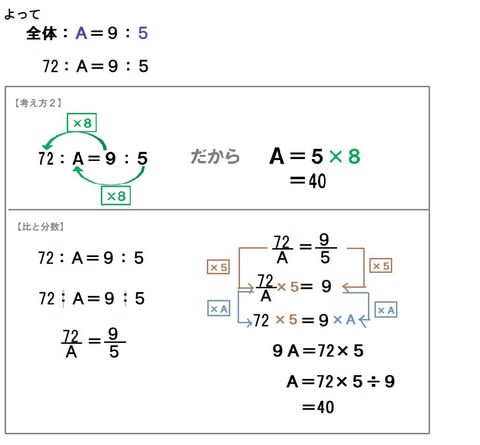
簡単な分数で考えてみると 1÷5 = 1/5 比の問題(小6)「比と分数の関係③」 今日は、 比 (小6)のちょっとした問題をやってみましょう。 「比と分数の関係③」 では、問題をやてましょう。 のxの値を求めよ。 この問題は考え方2と比と分数によって解くことができます。 面積が72 比と前項(後項)の値から後項(前項)の値を求めることができる。 評価規準 比の性質や図を用いて比の一方の値を求める方法を考え、説明している。(数学的な考え方) 問題 ケーキを作るのに、砂糖と小麦粉の重さの比が5:7になるように混ぜます。
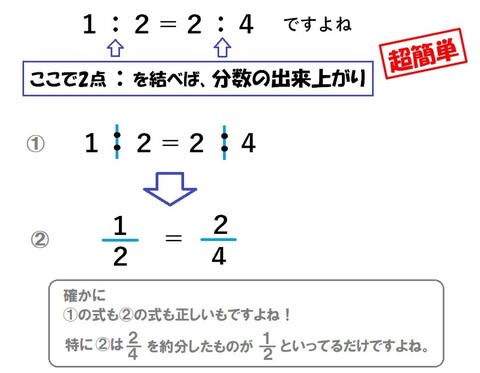



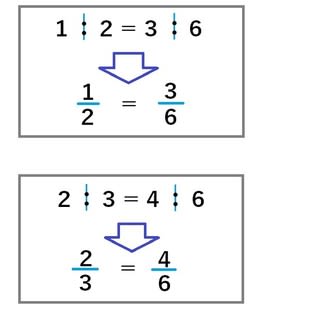
比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support
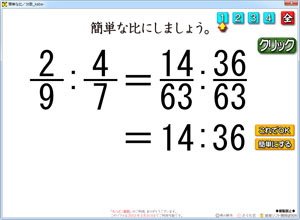



分数の比のソフト もうすぐアップします さくら社
中学受験 5年 unit 5 いろいろな文章題1 集合・和と差 つるかめ算・つるかめカブトムシ算 差集め算 過不足算・平均 中学受験 5年 unit 6分数は 比 や 割合 といった概念に対応しており、0 でない数 a を分母と分子にそれぞれかけても割っても、その分数の表す数は変わらない。 n m = n × a m × a = n ÷ a m ÷ a ( a ≠ 0 ) {\displaystyle {n \over m}= {n\times a \over m\times a}= {n\div a \over m\div a}\quad (a\neq 0)} m と n小数・分数の比 0016 テーマ: 算数嫌い解消! みなさん、こんにちは。 算数ギライをなくす活動をしているゼロ先生です。 いつもお読み頂きありがとうございます。 前回は、できるだけ小さな整数の比、つまり、「比を簡単にする」ことを
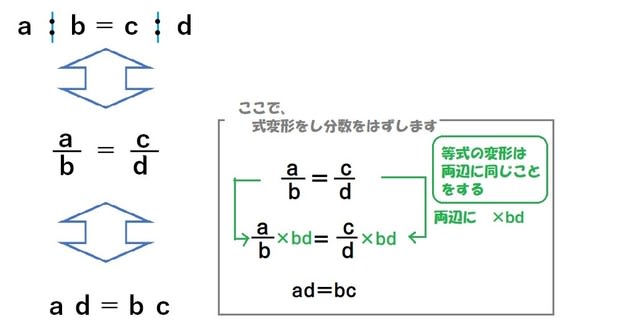



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ
比例式とは下のような2つの比が等しいですよ、 ab = cd ということを表した等式のことですね。 どういうときに2つの比が等しいっていえるかというと、比の値が等しいときなんです。 比が ab のとき 比の値は a/b になります。相似を表す記号 4ABC と4DEF が そうじ 相似のとき 4ABC ˝ 4DEF と表す. 三角形の相似条件 a b c ka kb kc a b ka kb 三角形が相似になる条件は次である. 1 3 辺の辺の比がすべて等しい ˆ 相似比1 k 2 2 辺の辺の比とその間の角がそれぞれ等しい ˆ 相似比1 k 等式の性質 等式の性質は4つあり、どれも重要な性質です。 1つ1つ確認していくのですが、等式の性質を説明していく上で必要な用語を追加しておきます。 それは「左辺」と「右辺」という用語です。 以下の図を見てください。



Core Ac Uk Download Pdf Pdf




比の計算問題 比を簡単にする方法は小学生でもできる 中学や高校の数学の計算問題
2 5 の 比の値の計算式 は 2 ÷ 5 となります。 よって $ 2 \div 5 = \frac{2}{5} (= 2 5 の比の値) $ なので、 2÷5 のわり算 ・ 2/5 の分数 ・ 2 5 の比の値 は 同じ数 を示しています。 図でイメージ わり算と分数のイメージ $ 2\div5 = \frac{2}{5} $ のイメージを 線分図 に書くと、 2の長さを 5つに分ける(上図 今回は小学6年生で習う「比とその利用」について勉強します。 比の性質を使い、整数だけでなく小数や分数の比を簡単にする方法について学んでいきたいと思います。 比を簡単にする方法 比を簡単にする問題 問題① 問題② 問題③ スポンサードリンク (adsbygoogle = windowadsbygoogle ) 例題(2)を比例式の性質を利用して解く 比例式特有の扱い方で解く 条件式が3つの比の値が等しいことを表す比例式であれば、式を変形するだけでは上手くいきません。ですから、 「=k」とおく比例式特有の扱い方 で解きます。



比の問題 小6 比と分数の関係 算数の教え方教えますmother S Math Happy Study Support



6年算数比とその利用2等しい比の教え方
・ 等しい比の意味を知り,その性質を 探る。 ・探究的な活動 ・説明する活動 知 等しい比の意味や性質を理解 している。 4 / 8 ・ 比の性質を使って,できるだけ小さ な整数の比になおす。 ・探究的な活動 ・説明する活動 技 等しい比の性質を利用して,で性質 比例式には、次のような性質がある。 = = 外項の積と内項の積が等しい(分数式で考えた場合、たすきに掛けた積が等しい)。 = = 関連項目 比; 「 3 5 」とは「 3 ÷ 5 」のことであり、これを「 比の値 」と呼びます。 そして、 \(3\div5=\displaystyle\frac{3}{5}\) と 分数で表せます 。 比の性質 「 A B 」のとき「 A と B に 同じ数を 掛けても ( 同じ数で 割っても) 比は等しいまま 」です。




分数のかけ算わり算 まとめ 小学生 算数のノート Clear
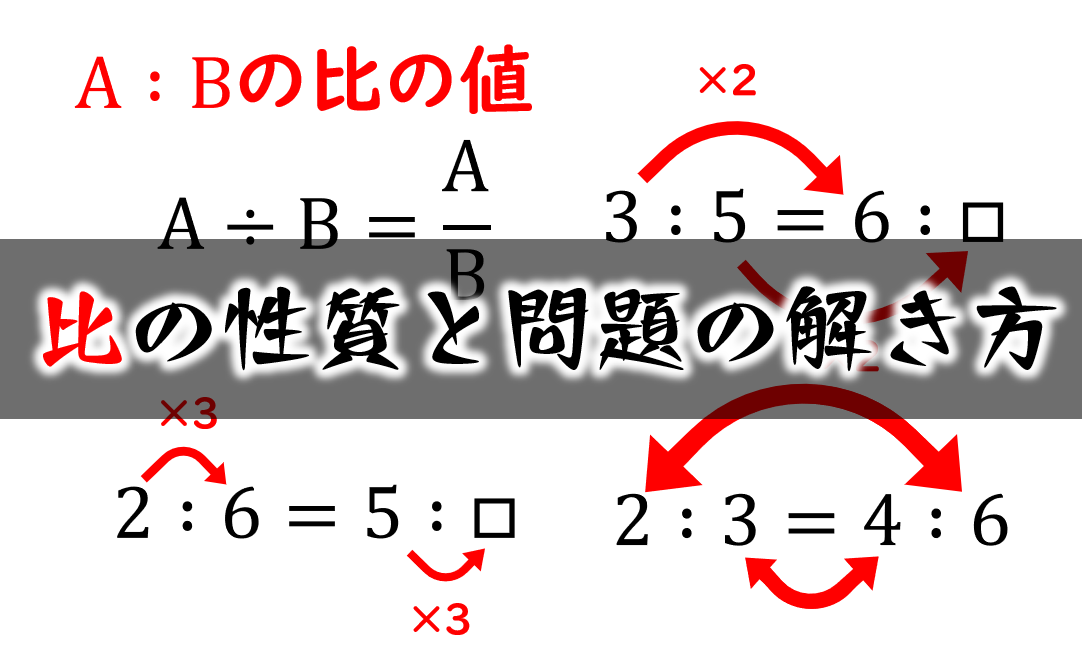



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun
数学A /図形の性質「平面図形」 5 / ??分数のわり算は、以下のように計算しますね。 4 ÷ 2 5 = 4 × 5 2 = 10 この式だけで説明しようとすると理解しにくいと思いますので、まずは簡単な こんにちは、ウチダです。 今日は、中学1年生で習う 「比例式」 について、まず分数を用いた計算方法からある重要な公式を導き出します。 また、記事の後半では、かっこを含む比例式の計算を要する文章問題なども解説していきます。 比例式とは 比例式を理解するには、"比"という考
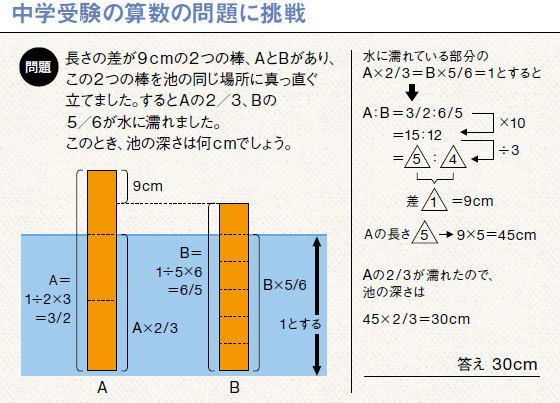



比とは何か を子どもに説明できますか 当社の顧客の男女比は7 3です President Online プレジデントオンライン
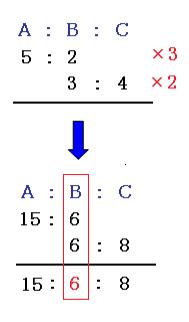



比の性質を解説 比例式や連比の解き方だってこんなに簡単




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




6年生算数ドリル 割合を表す分数
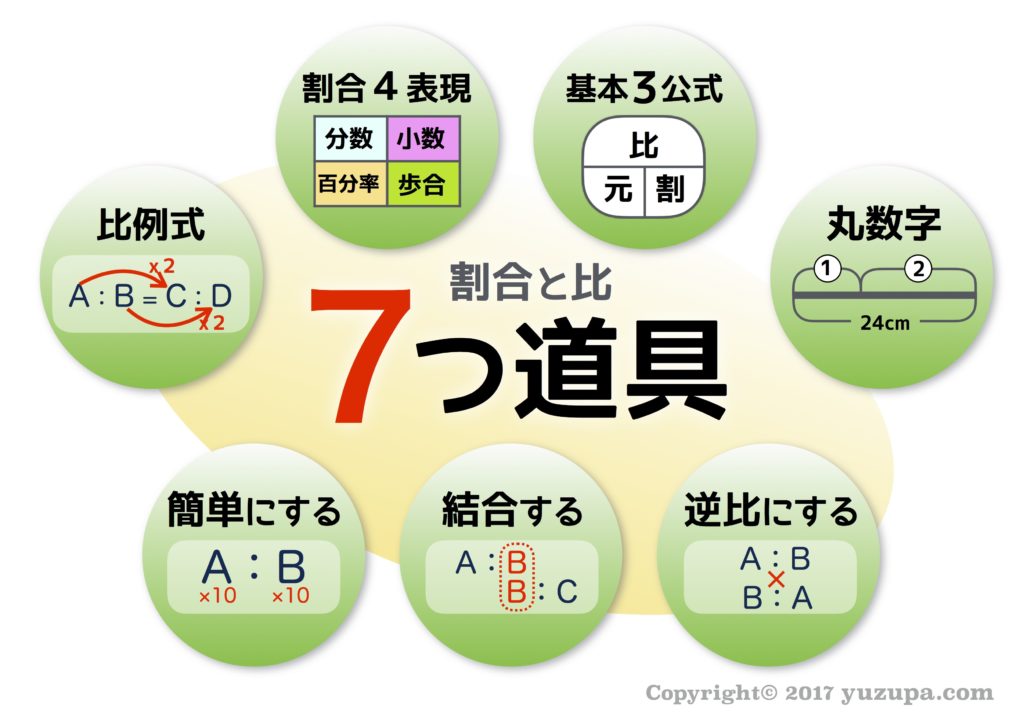



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




比例式の解き方とは 分数を用いた計算 かっこを含む文章問題をわかりやすく解説 遊ぶ数学



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun



1
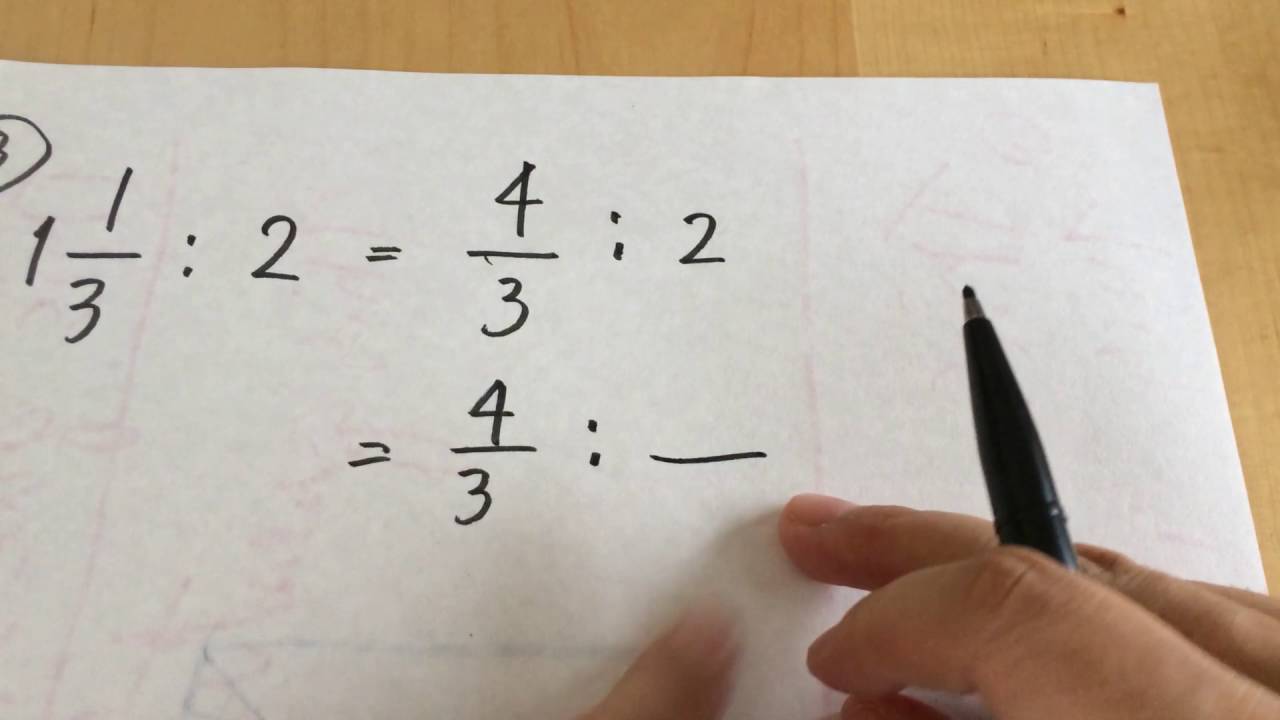



比を簡単にする Youtube




比の計算はこれで完璧 比の値の求め方と考え方



算数小6の問題です 分数の比を簡単にするという問題です 6 Yahoo 知恵袋




分数がわかれば割合もわかる 割合 比 確率の共通点 カテガクブログ



わり算2 オイラーに習う分数の割り算 大学への算数 Ena国際部
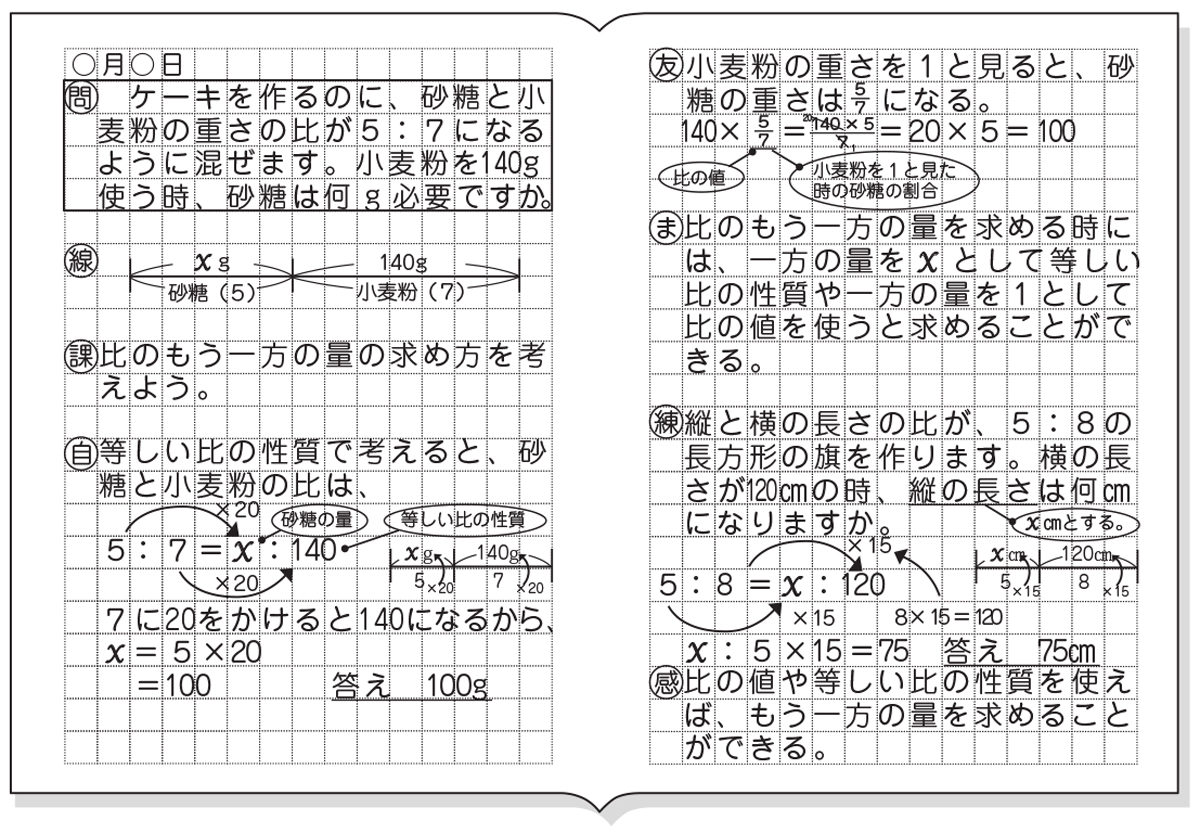



小6算数 比と比の値 指導アイデア みんなの教育技術
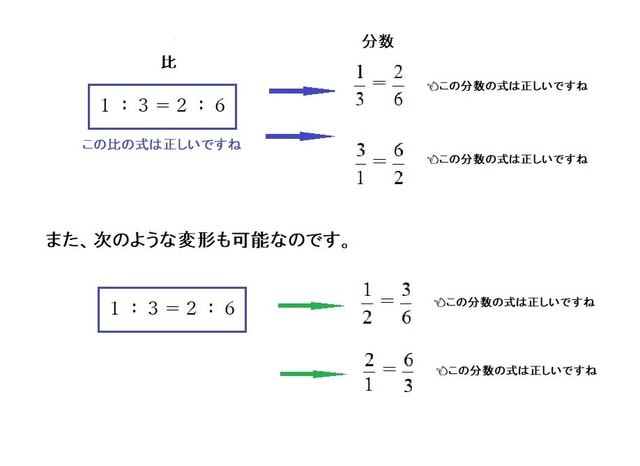



超重要 中学数学の分数準備7 比と分数 算数の教え方教えますmother S Math Happy Study Support



6年算数比とその利用2等しい比の教え方
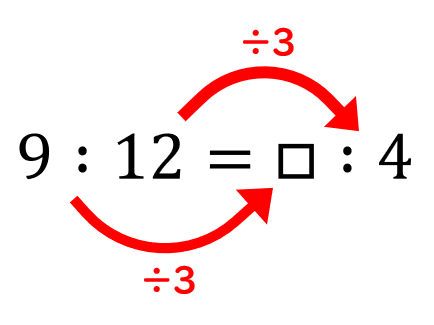



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




比とは何か を子どもに説明できますか 当社の顧客の男女比は7 3です President Online プレジデントオンライン



2



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




小学校5年生の算数 数学fun 勉強 本 分数 算数




比と比の値についての自主学習ノート例 家庭学習レシピ




比例式の性質 3分でわかる 比例式の解き方 Qikeru 学びを楽しくわかりやすく



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html




6年生算数ドリル 比と比の値



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋



3




小学6年生 算数 比2 等しい比の性質 Youtube



1
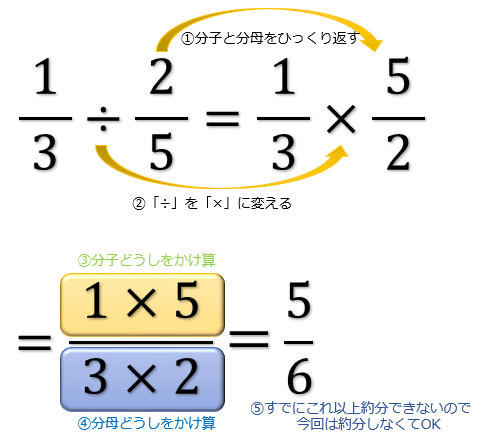



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ
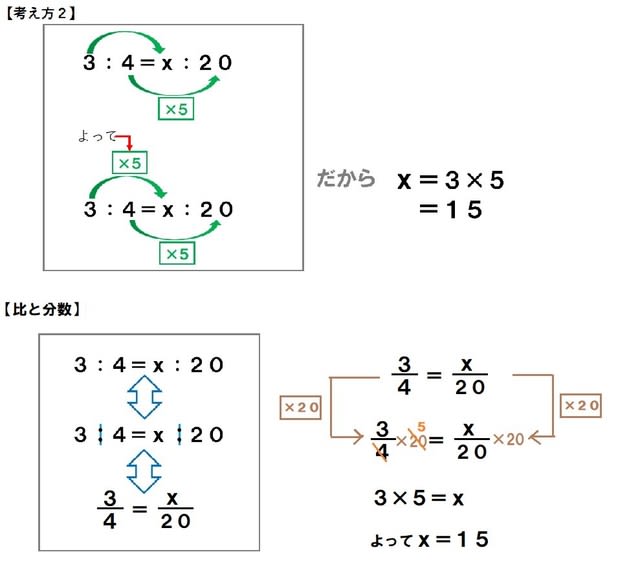



比の問題 小6 比と分数の関係 算数の教え方教えますmother S Math Happy Study Support



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html




比の基本操作を3つをマスター
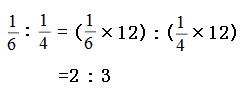



比の性質を解説 比例式や連比の解き方だってこんなに簡単



Http Www Torikyo Ed Jp Kyoiku C H29ad 04 3 Pdf




6年生算数ドリル 比と比の値



比と比の値 算数用語集




比を簡単にする から比は始まる




比の性質を解説 比例式や連比の解き方だってこんなに簡単




メルカリ 数研出版 学ぼう 算数 高学年用 下 推奨学年 6年 参考書 800 中古や未使用のフリマ



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




比と比の値についての自主学習ノート例 家庭学習レシピ



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support




比を簡単にする方法 小学生 中学生の勉強




比の値って結局なんなの 苦手な数学を簡単に




小6 算数 小6 16 比と比の値 Youtube




比



逆数とは 逆数の意味や求め方 逆数の和などの計算問題 受験辞典



3




中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




連比の問題と解き方のテクニック3つ Youtube音声動画付き 中学




数学塾直伝 分数の割り算の教え方と詳しい理屈 どうしてひっくり返すのかがよくわかる 永野裕之のblog



分数と比が苦手な人のための 法 ニャース滝の 猫が長靴をはいたなら



Www12 Schoolweb Ne Jp Weblog Files C0065 Doc 4669 663 Pdf



6年算数比とその利用2等しい比の教え方



算数実践実例集 啓林館



小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生
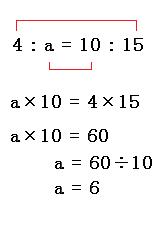



比の性質を解説 比例式や連比の解き方だってこんなに簡単




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




逆比の例と計算 分数 小数 3つ以上の数の比の逆比 中学数学 Irohabook




小6 算数 小6 15 比と比の値 Youtube
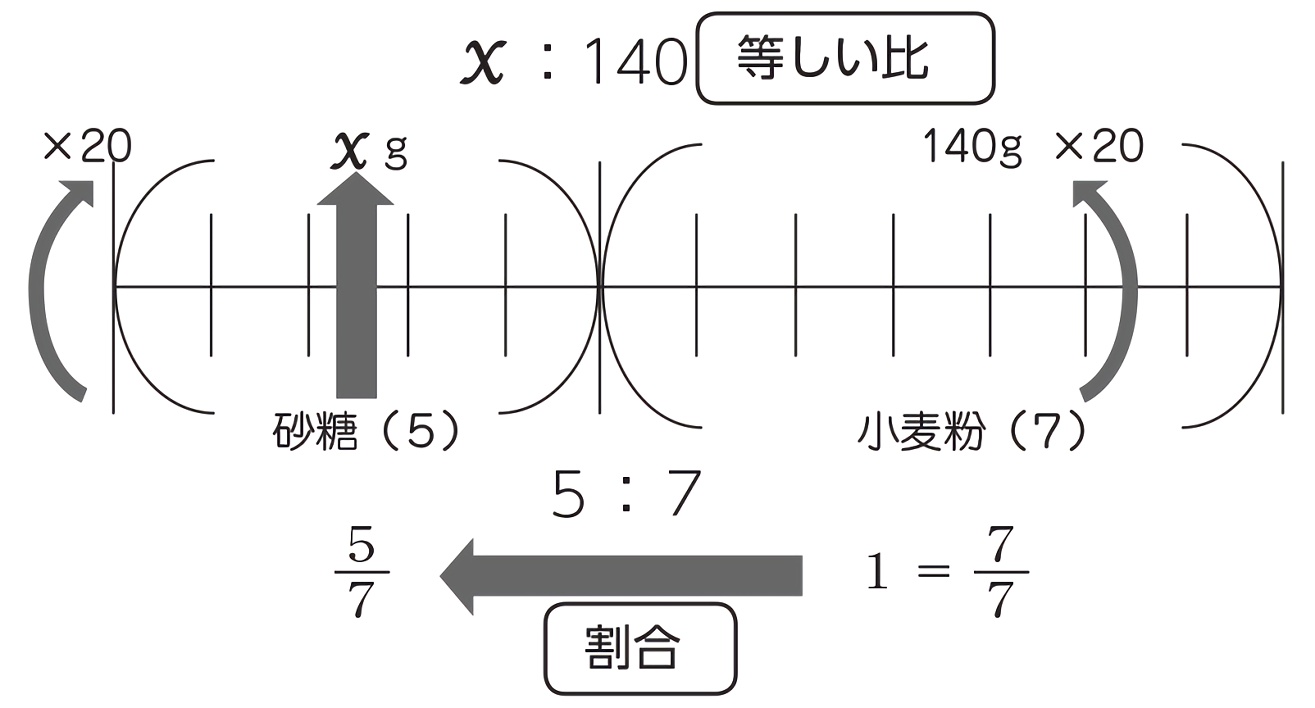



小6算数 比と比の値 指導アイデア みんなの教育技術



わり算2 オイラーに習う分数の割り算 大学への算数 Ena国際部



2




高校数学b 整数mとnの間にある分母pの既約分数の和 受験の月




高校数学 循環小数から分数への変換 0 999 1 受験の月




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun




小学総まとめ 比 きっずゼミ子育て応援ブログ




比と比の値 その2 家庭学習レシピ




比と比の値についての自主学習ノート例 家庭学習レシピ



楽天ブックス 中学受験のための1日5題 まいにち算数 90回でほんもの実践力 みくに出版編集部 本
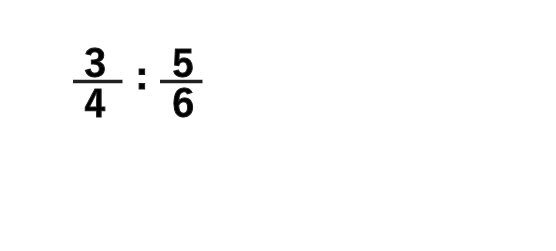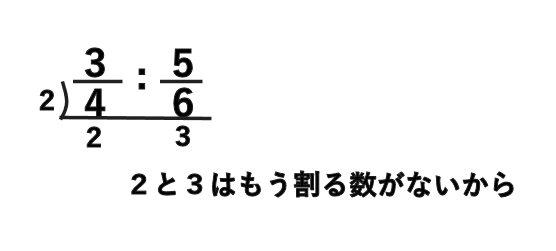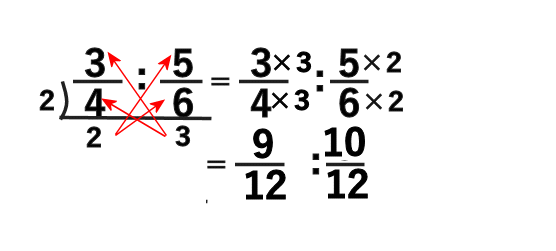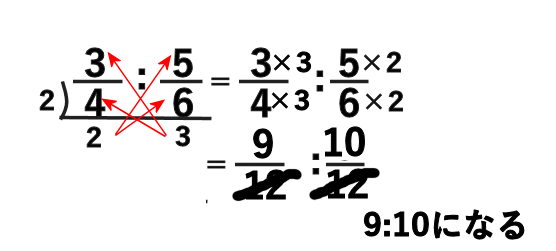



分数の比を簡単にする




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun



分数がわかれば割合もわかる 割合 比 確率の共通点 カテガクブログ



1 8 4の比の値を分数で答えなさいを教えてください 比の値を Yahoo 知恵袋




すきるまドリル 小学6年生 算数 比と比の値 比と比の利用 無料学習プリント すきるまドリル 無料学習プリント



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Bunsu Html




小学校6年生の算数 数学fun 算数 分数 数学




比を教える



Core Ac Uk Download Pdf Pdf




中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




小6 算数 比と比の値 解説 動画 Youtube




割合 百分率 比の概念




三角形と比で苦戦するのはなぜ つまずきやすいポイントとその解決策を紹介 中学受験ナビ



0 件のコメント:
コメントを投稿