単元:等式の変形問題の解き方 問題 次の等式を,の中の文字について解きなさい。 中学生数学特訓プラン 基礎力養成特訓プラン 推奨学年中学1年~中学3年生内容計算の基礎養成演習時間割50分授業×週1回方程式1+2y =6を解き,その解き方にしたがって,等式x +2y =6をy に ついて解く活動を取り入れることが考えられる。 目的に合うように等式を変形することの意味を理解するために,具体的な 事象と関連付けられるようにすることが大切である。 中学数学の教え方について、具体的に解説するこの連載。 今回は中2数学「等式の変形」です。 やり方を示しても、自力ではできない。 分数まじりの難問になると、解き方の順番がめちゃくちゃ。 なぜこうなるの?わからないと言ってくる。
等式の性質とは 方程式を解くための考え方を身につけよう 方程式の解き方まとめサイト
等式の変形 解き方 分数
等式の変形 解き方 分数-N=4ab3 (←手順1:分数・かっこを計算) 4ab3=N (←手順2:左辺・右辺入れ替え) 4ab=N+3 (←手順3:解く文字の入った項以外は全て右辺へ(符号に注意!)) a=(N+3)/4b また、この変形の仕方を身に付ければ、様々な公式に利用することができます。分数の分数乗の解き方を教えてください 数学 高校生 約3年前 e 分数の分数乗の解き方を教えてください 0 回答 ちるむ 「二次関数の理解」を最大値まで完璧にするノート3選 文系だって超わかる!




文字式の利用 等式変形の実践問題を解いてみよう 中学数学をはじめから分かりやすく
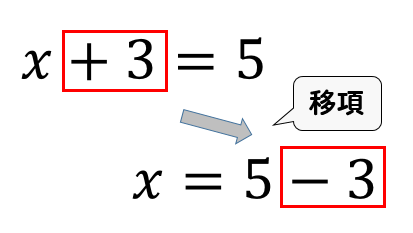
④ 等式の性質を文章と式とでまとめる。 ↓ 7 図・表・式・グラフに表現した り,よみとる。 2 帰納的に推論する ⑤ ①~③の方程式の解がどれも5であることから,方 程式は,等式の性質を使って同値変形できることを帰 納的に理解する。 準備するもの等式の変形 代入法による解き方 代入法による解き方の応用 加減法による解き方 加減法による解き方の応用 小数と分数を含む連立方程式 工夫して解く連立方程式 定数を含む連立方程式 a=b=cの形の連立方程式 連立方程式の利用等式変形(〜について解く)は、移項に注意 投稿日:年6月13日 等式(すでにイコールがついた式)を変形させる「等式変形」についての解説です。 例えば、辺の長さから面積を求める式を組み替えて、面積から辺の長さを求める式へと変化させること
中学2年等式変形 解き方 ※現在日本語と韓国・朝鮮語、中国語、ポルトガル語、ベトナム語に対応しております。 韓国・朝鮮語|中国語|ポルトガル語|ベトナム語|フィリピノ語|英語絶対値記号を含む方程式・不等式の解き方 A| x +3|=4 B | x +3|=4 x C | x +3|<4 D | x +3|≧4 x の解き方を教えてください。 進研ゼミからの回答! こんにちは。 いただいた質問について,さっそく回答いたします。 次の等式を、( )内の文字について解きなさいとゆう数学の問題の解き方を教えて欲しいんですけど下の3つが問題です。2x3y9=0 y½ ab=4 (a)L=2(mn) (m)2x3y9=0 2xと9を移項します3y=2x9 両辺に1/3をかけます3
000 000 / 345 Live • ① p = 5 4 ax 2 y 左辺と右辺を入れ替える 5 4 ax 2 y = p 両辺に 5 4 の逆数をかける ax 2 y = 4 5 p 両辺をax 2 でわる y = 4p 5ax 2 分数がある場合は文字と数をわけて、まず分数の逆数を両辺にかけるとよい ② S = 2 3 ax – 5k 左辺と右辺を 分数式の恒等式の問題の解き方 分数式が恒等式となる定義は, 分母を払った式が恒等式になること です。定義なので「なんで?」はありません。 よく分母が0になる$\ x\ $の値はどうなるのかといった議論をする人がいますが、これは不毛な議論です。等式 xy=5 を x=5 y に変形したり, S= を h= に変形することは, 次に習う方程式の解き方において基本となる技術です.




恒等式とは何か 恒等式を使った問題の解き方について アタリマエ




中2数学 等式の変形の解き方と練習問題 Pikuu
中2数学「等式の変形の解き方と練習問題」 中2数学「等式の変形」方程式のように解くことがポイント! についてまとめています。 等式の変形は、中学1年生で学習した「一次方程式を解く」という単元のポイントとほぼ同じです。 目次 等式の変形中1数学のポイント、「方程式」。解き方の基本、「移項」って何? なぜ符号が変わるの?? ぜんぜん分からん(泣)。おや、中学生が倒れそう。立て、立つんだトォォォ~ッ! オール5家庭教師、見参ッ! 「方程式」のコツを一発解決! 無料サイト。 分数関数とは? グラフや微分・積分、不等式の解き方 21年2月19日 この記事では、「分数関数」についてわかりやすく解説していきます。 グラフの書き方や不等式の解き方、微分・積分の計算なども説明しますので、この記事を通してぜひマスターして
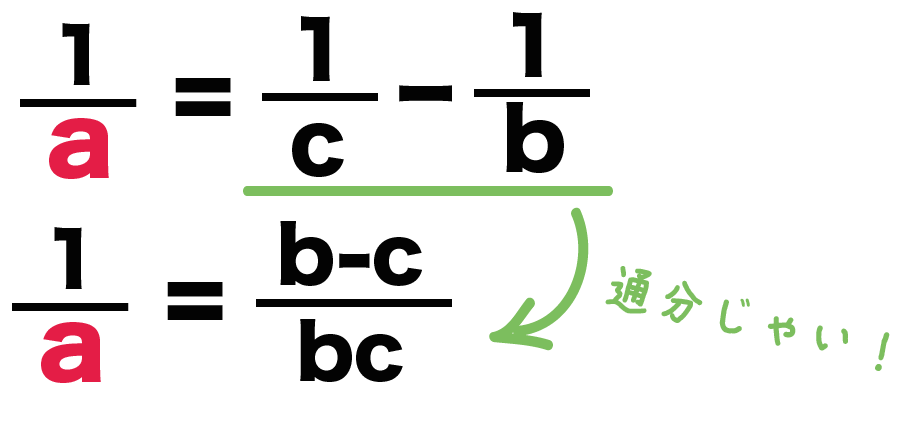



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




世界一わかりやすい数学問題集中1 3章 方程式
分数を伴うのが苦手の事なので、 (2)を例にして解きますね 2a7b a=一一一一一 解き方は何種類かあります。 3 ① 右辺は言い換えれば (2a7b)÷3 よって、先ず3を移項して、 3a=2a7b 2aを移項して a=7b bについて解けば b=a/7それは分母に があっても同じこと こうすることによって、方程式を普通の形に変形することができます! それでは、このやり方で方程式を解いていきましょう。 両辺に を掛けると 両辺に を掛けると 両辺に を掛けると 両辺に を掛けると方程式を解くとは、等式の変形を上手に行って、 x = x = 数値 というところまで式変形をすることです。 そのさい、移項を用いて、 式変形の手間を少しだけ減らすことができます。 方程式の解き方をまとめます。 移項によって、左辺に x x の項を集める




中2数学 等式の変形の解き方と練習問題 Pikuu




Akiya Su 数学 文字と式 等式変形 文字式の逆数がわからない人が多い印象 一次関数で必要な知識なので是非身につけてください 中学数学 文字と式 等式変形 数学
分数を使った等式の変形の解き方 邪魔な分数をかけ算で消しちゃう 内の文字について解きなさい 分数が邪魔なので、まずは分数を消してしまいましょう。 4と6を消すためには、最小公倍数である12をかける必要がありますね。 ここでは、方程式を解くために利用できる、等式の性質について見ていきます。 方程式を解く 基本方程式とその解では、次のような方程式を考えました。 1x140=500 方程式とは、文字に代入する値によって、 分数の移行について質問です なぜこの様になるのでしょうか 中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを 等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 1次方程式の解き方 文字の分数の計算を習う学年 文字の分数の




2 10型 1次分数型 の漸化式 おいしい数学



Www Nier Go Jp 12chousa 12kaisetsu Chuu Suugaku Pdf
実は,この分数不等式は 方法1.分母を払う方法 以外にも 方法2.通分する方法(おすすめ) や 方法3.両辺のグラフを描く方法 といった解き方があります。 以下では,3つの方法をそれぞれ解説します。 等式の変形練習問題 左辺を だけにしたいので、 を右辺に移項します。 が右辺にあるので、まずは左辺と右辺を入れかえてからスタートすると計算がしやすくなります。 次に、 を右辺に移項しましょう。 の係数である3を消すため、両辺を3で割り について解くので、最終的な形は「 」になります。 では、方程式の解き方のSTEPに従って等式変形をしてみます。 今回、 ( )や分数、小数は無いのでSTEP3「移項」からです。 着目する文字は です。 つまり、片方の辺に を含む項、もう片方の辺にそれ以外
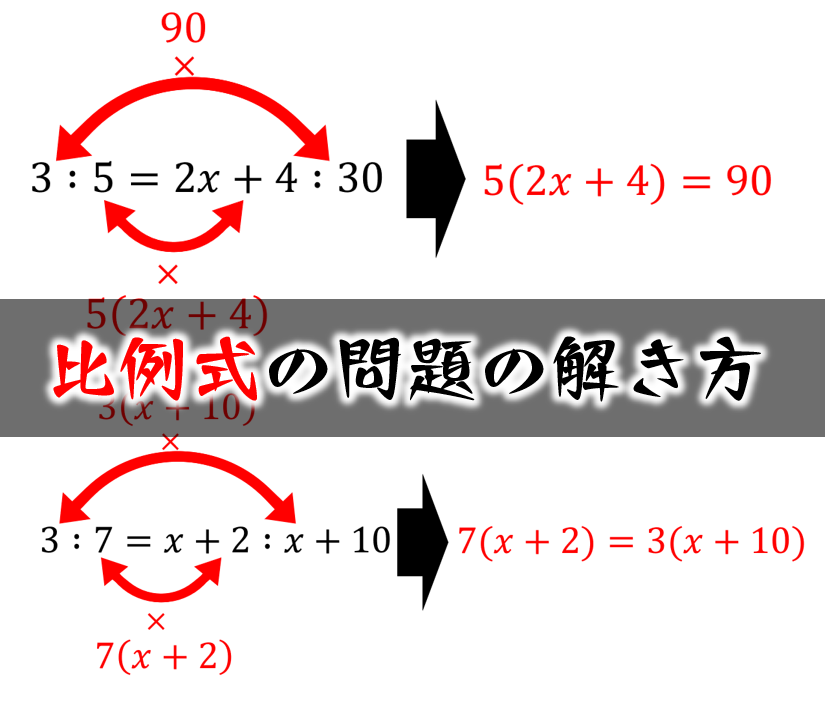



比例式の問題の解き方 数学fun




等式変形 について解く は 移項に注意 あんず学習塾のメモ 図表置き場
Home / 中学1年 / 数と式 / 中学1年等式の性質 等式変形 中学3年二次方程式を解くこと 平方根の考えを使った解き方 年4月8 相等 不等式 中国語 中央値 中学1年 中学2年 中学3年 二元一次方程式 二等辺三角形 代入法 代表値 分数 という形に変形していくのが鉄則です。 そのためには ①分数を取っ払う ②左辺に解きたい文字だけを集める ③解きたい文字を括る ④解きたい文字の係数で割る というのが基本的な解き方です (ただし例外もあるので (2)で説明します) (1) a 1 b = 5 の b中2 式の計算 等式の変形 (かっこを含む式) 方法1:分配法則でカッコを開いて計算 2 (p−2k) = A ←カッコを開く 2p−4k = A ←−4kを移項 2p = k ←両辺を2で割る p = k 2 A 2 2kとしても良い 方法2 カッコの外の2で両辺を割ってから




等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ




漸化式の解き方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
等式の変形1 1 ( )内の文字について解きなさい。 5x=P (x) 2xy=ac (y) 4P=3n (P) 3x2=R (x) ax1=y (x) 4ax2 =V (a) PR−2n=xy (P) cx−7=4nr (x) 2 ( )内の文字について解きなさい。 3xy=12 (y) 4ac=x2 (a) 5a3b=7c (b) 3 5 ax=p (x) 解説リクエスト 解説リクエストフォーム




中2数学 式の計算 等式の変形 4つのパターンで必ず解ける たけのこ塾 勉強が苦手な中学生のやる気をのばす



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典



Http Www Center Ibk Ed Jp Action Common Download Main Upload Id 3567




等式の変形 Youtube




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学



1




文字について解く 等式の変形 問題 Youtube




練習問題 等式の変形の解き方 やり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



等式変形で質問です Y Axをaについて解けという問題で両辺をxで Yahoo 知恵袋



分数関数とは グラフや微分 積分 不等式の解き方 受験辞典




中学数学2年 等式の性質と等式の変形 移項 文字について解く 受験の月




例題付き 連立方程式の解き方と失敗しないコツ
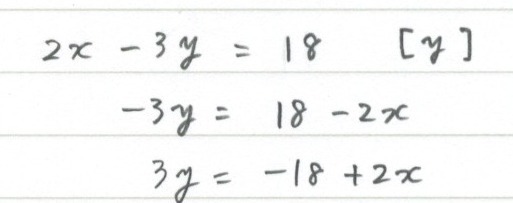



4 6 式の計算 等式の変形 勉強できようサイト




分数のたし算の問題 面白い解き方が沢山あるのでまとめました Math Channel Note




中学1年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学校数学科学習指導案 1 題材名 2次方程式 2 題材について
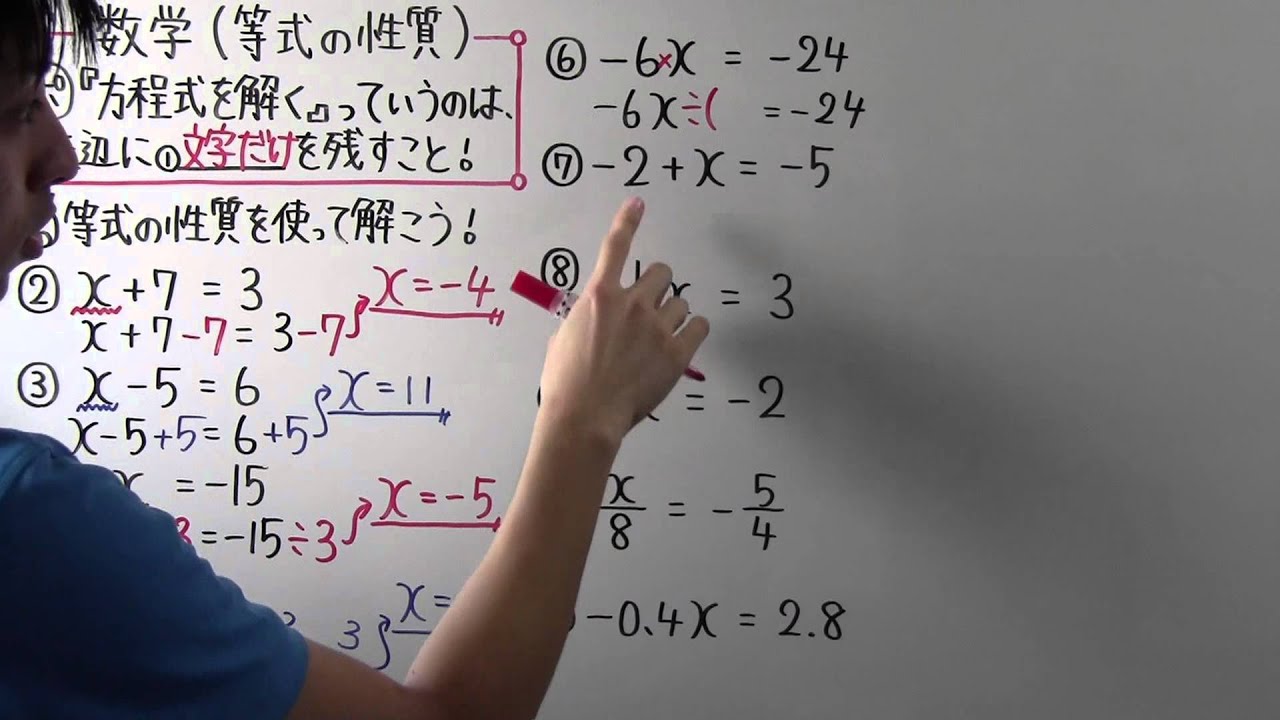



中1 数学 中1 27 等式の性質 Youtube




間違えやすい計算 分数 のポイントと解き方 現役塾講師のわかりやすい中学数学の解き方




中学生 数学 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
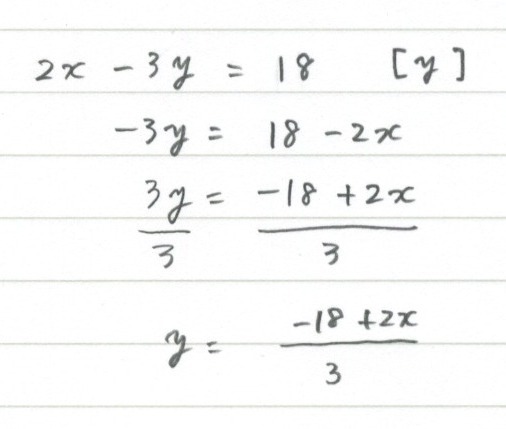



4 6 式の計算 等式の変形 勉強できようサイト
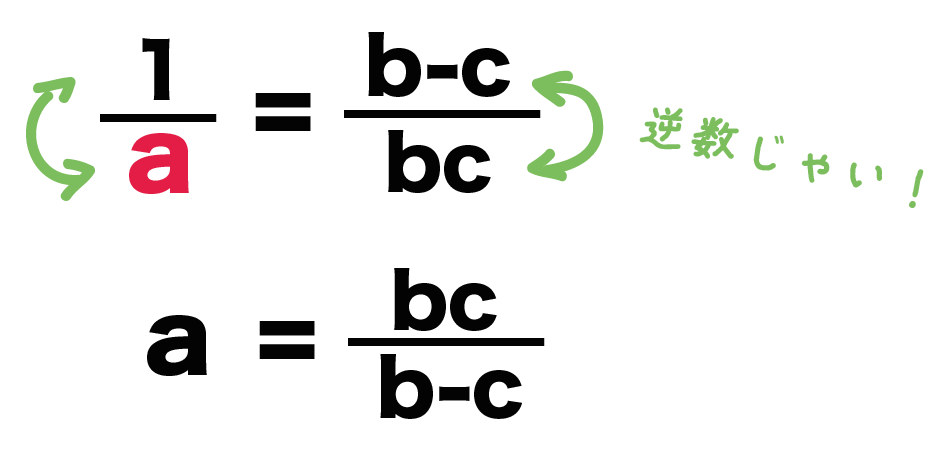



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく
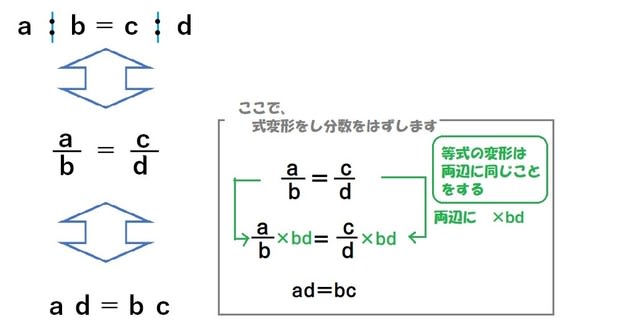



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support



楽天ブックス 自由自在中学数学 平成28年改訂 基礎から入試まで 河野芳文 本




高校数学 繁分数式 分数の分数 の計算 受験の月




等式の性質とは 方程式を解くための考え方を身につけよう 方程式の解き方まとめサイト




分数を使った等式の変形の解き方 成績プラス




連立方程式 代入法 無料で使える中学学習プリント




中学2年生 等式の変形 公式 個別進学教室マナラボ受験 教育情報サイト



等式の変形で分からない問題があります 解き方を教えてください Yahoo 知恵袋




中学数学 連立方程式 代入法 中学数学の無料オンライン学習サイトchu Su
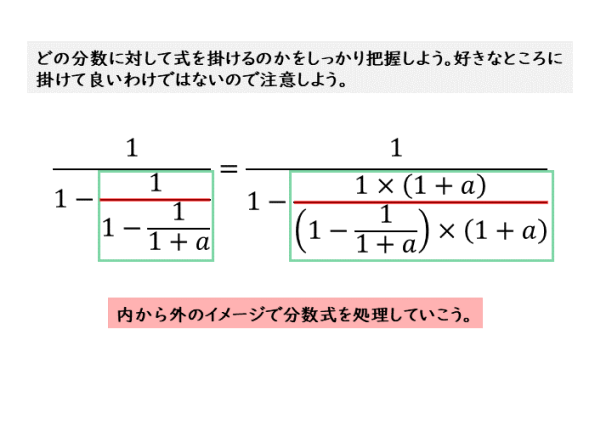



式と証明 繁分数式の計算について 日々是鍛錬 ひびこれたんれん



1




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ




数学 中2 8 Xについて解く Youtube



中2の数学 等式の変形なんですけど整数だけならまだわかるんです Yahoo 知恵袋



乗法公式とは 1分でわかる意味 公式の覚え方 問題 因数分解との関係




等式の変形 問題15題の練習と解説 分数などのパターンも 中学数学 理科の学習まとめサイト




比の計算問題 比を簡単にする方法は小学生でもできる 中学や高校の数学の計算問題
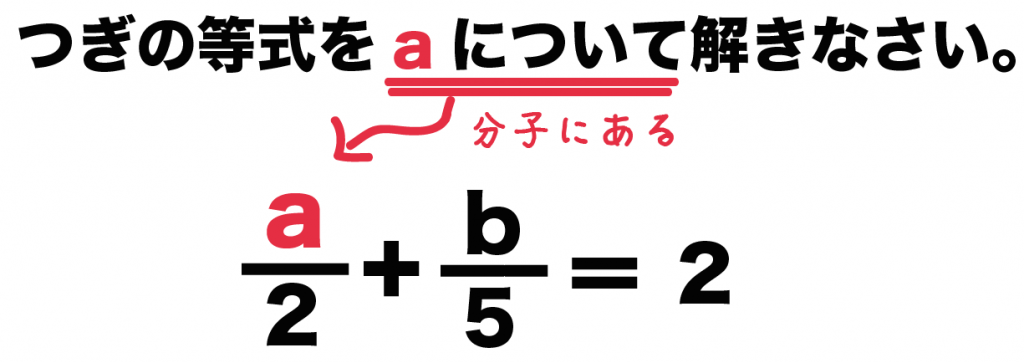



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく




不定方程式の解き方とは 全4パターンを東大医学部生がわかりやすく解説 東大医学部生の相談室




中2の数学の等式の変形の問題です 1 A 1 B 1 C をbについて解 人力検索はてな




等式の変形で 解き方を説明してくれませんか 分数などが含まれている等式が苦手です Clear
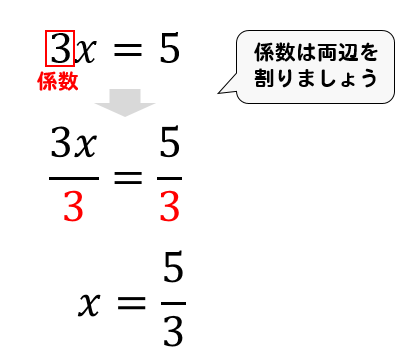



等式の性質とは 方程式を解くための考え方を身につけよう 方程式の解き方まとめサイト
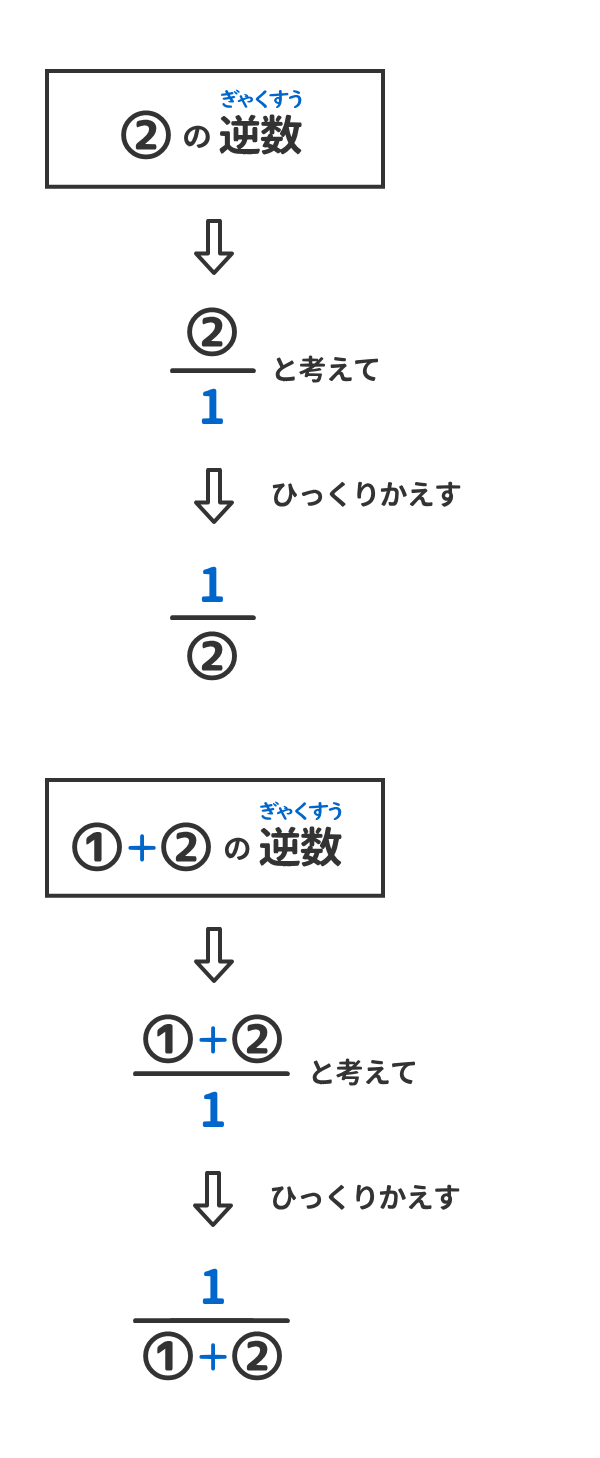



等式 の変形をして必要な情報を取り出そう 電験3種web




分数を使った等式の変形の解き方 成績プラス




中学数学 一次方程式




文字式の利用 等式変形の実践問題を解いてみよう 中学数学をはじめから分かりやすく




高校入試 等式変形の入試問題を挑戦してみよう 数スタ



Math 超簡単 等式の変形 文字について解く 働きアリ




練習問題 等式の変形の解き方 やり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中2数学 等式変形のやり方 ひっそりと物理や数学を解説する
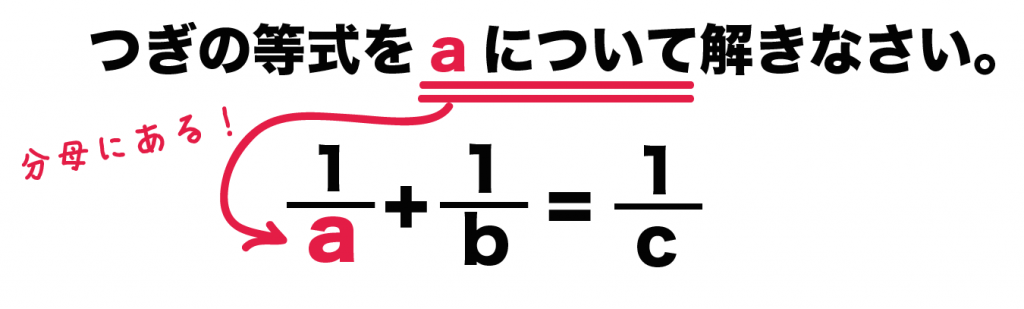



中2数学 分数がふくまれる等式の変形の2つの解き方 Qikeru 学びを楽しくわかりやすく



方程式の移項のナゾを解いてみよう 算数 数学 英語塾のフェルマータ




4 6 式の計算 等式の変形 勉強できようサイト




等式の変形 無料で使える中学学習プリント




等式の変形 解き方のポイント 現役塾講師のわかりやすい中学数学の解き方




比例式の解 計算ドリル 問題集 数学fun



不等式の解き方 Gains ゲインズ ネットスクールの資格取得応援情報サイト
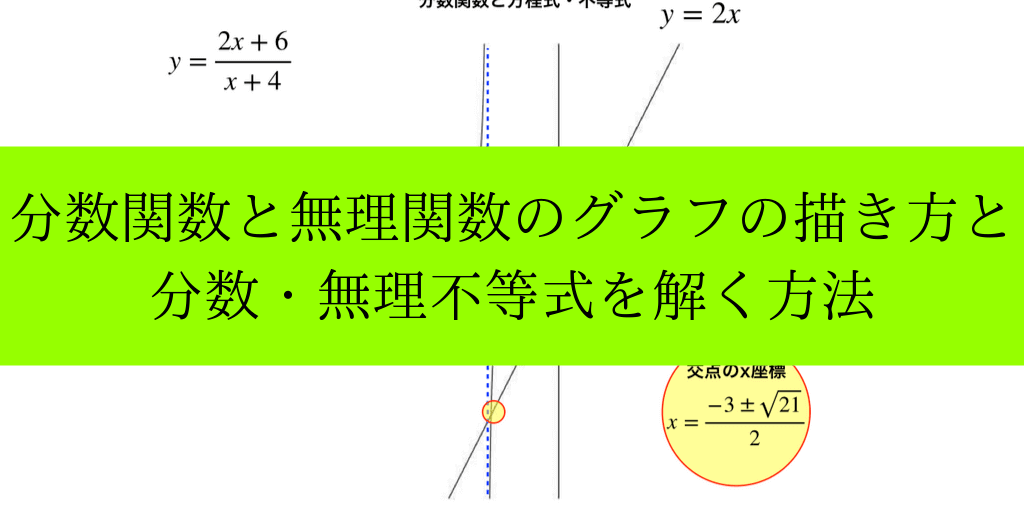



分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



1




式の計算 中2で学ぶ式の値の実践問題を解いてみよう 中学数学をはじめから分かりやすく




ルートの応用問題 を変形して 計算できるようにする 中学や高校の数学の計算問題




高校数学 因数分解 4乗が登場する式の因数分解 置き換えをして見慣れた形に直して解こう 数学の面白いこと 役に立つことをまとめたサイト




一次方程式の解の求め方 数学fun




中学数学 等式の変形 でつまずく原因と 効果的な教え方



中二 等式の変形




等式変形 について解く は 移項に注意 あんず学習塾のメモ 図表置き場




中2 中学2年生 数学 Xについて解く Yについて解く 中学生 数学のノート Clear




中学数学 等式の変形 でつまずく原因と 効果的な教え方




等式変形 について解く は 移項に注意 あんず学習塾のメモ 図表置き場



等式の変形のやり方 中学2年数学 式の計算



Http Kore Mitene Or Jp Tohru Eq 00 Pdf



Www Dainippon Tosho Co Jp Math Files Pdf R2 Sugaku2 Sk Pdf



Http Www Town ami Niigata Jp Living Sc Images Mathplan Pdf



中2の数学 等式の変形なんですけど整数だけならまだわかるんです Yahoo 知恵袋
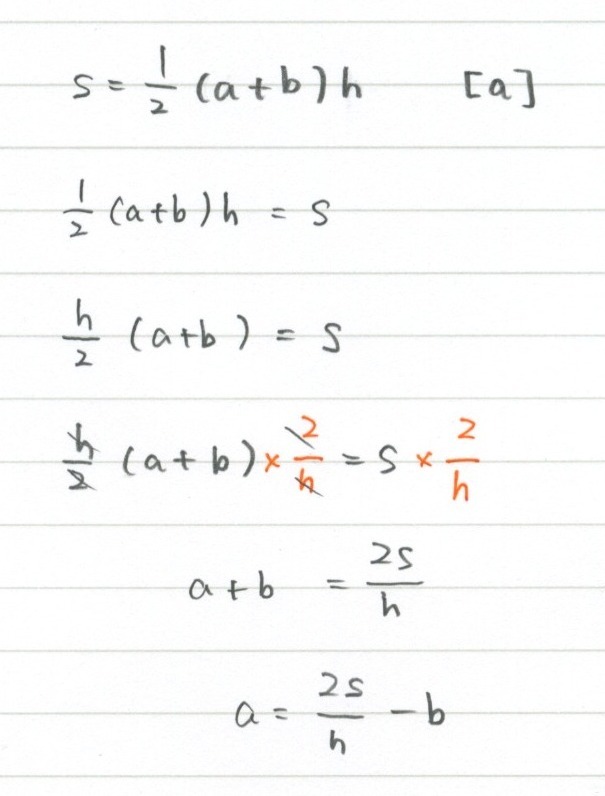



4 6 式の計算 等式の変形 勉強できようサイト
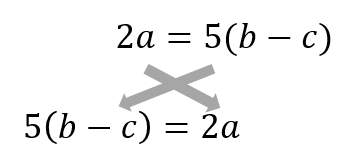



等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ
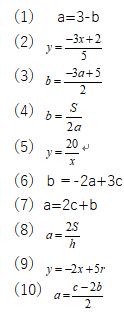



中2数学 等式の変形の解き方と練習問題 Pikuu




高校数学 三角比の等式を満たす三角形の形状決定 受験の月
(%E3%80%80)%E2%97%8F.png)



中学数学 二次方程式




絶対値記号を含む方程式 不等式の解き方 数学 苦手解決q A 進研ゼミ高校講座




中1 1次方程式 でつまずく原因と解決法 導入



Www Pref Oita Jp Uploaded Attachment Pdf




絶対値記号を含む方程式 不等式の解き方 数学 苦手解決q A 進研ゼミ高校講座
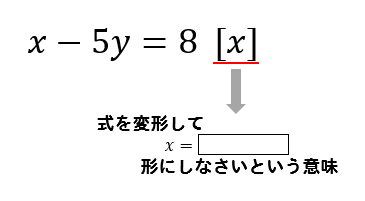



等式の変形 分数 かっこなど 解き方をパターンごとに問題解説 数スタ



不等式の解き方 Gains ゲインズ ネットスクールの資格取得応援情報サイト



48s96ub7b0z5f Net Gojoho Futeihouteishiki



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス



3



分数 文字式 約分
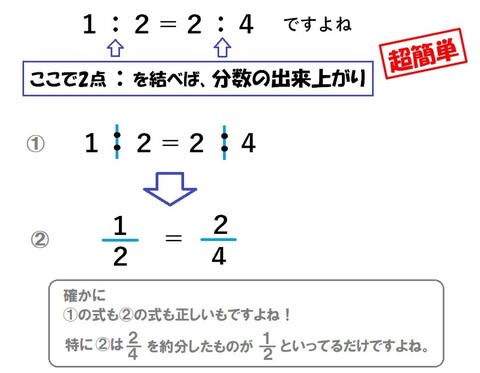



比と分数の関係 小6 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿